所谓凸包，即平面上存在若干个点p，通过若干个点形成的凸多边形可以包围平面上的所有点。

下文以力扣题目587. 安装栅栏来说说蒟蒻学习该算法的过程以及解题思路

上图中的各点坐标为

points = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]

思路

# 凸包算法（QuickHull
  1. 找横坐标最小值x1，最大值x2，记p1，p2
  2. 以p1、p2两条做直线，将凸包分为上凸包和下凸包
  3. 以上凸包举例，在位于p1、p2直线上方的点中获取点pm点，使得pm到p1p2的距离最大
  4. 取上凸包点的工作分为直线p1pm和pmp2，重复2~3步骤

其中，找两端的端点非常简单，只需要对输入的点数组进行排序即可。

通过两个端点，划分上下凸包，如下图所示

计算直线方程，写成y=k(x-x0)+y0的形式

由两点式：

$$\frac{x–x_1}{y–y_1}=\frac{x_2–x_1}{y_2–y_1}$$

直线方程：

$$y=\frac{y_1–y_2}{x_1–x_2}(x–x_1)+y_1$$

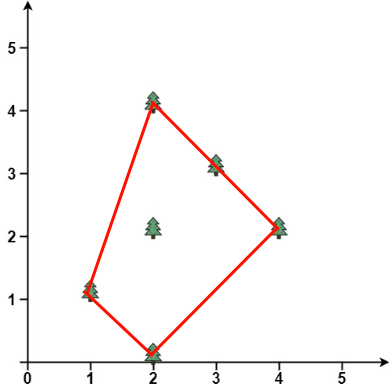
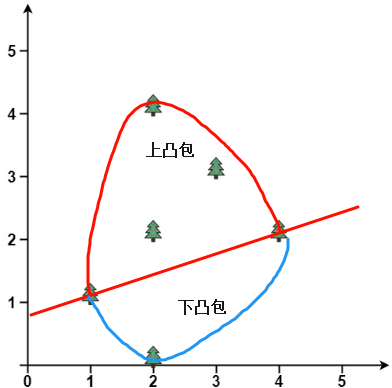
遍历点数组，带入方程，y值大于直线时，加入上凸包，小于直线时，加入下凸包，详细见代码：

def hull(points: list[list] = [], p1: list = [], p2: list = [], isUp: bool = True) -> list[list]:
    '''获取上(下)凸包中的点'''
    hull_points = []
    for p in points:
        x0, y0 = p[0], p[1]
        x1, y1, x2, y2 = p1[0], p1[1], p2[0], p2[1]
        if x1 == x2:
            continue
        y = (y1-y2)/(x1-x2)*(x0-x1)+y1
        if isUp and y0 >= y:
            hull_points.append(p)
        if not isUp and y0 <= y:
            hull_points.append(p)
    return hull_points

这里简要说明一下传入参数，points为当前处理的点数组，p1、p2为当前的两个端点，isUp表示是处理上凸包还是下凸包，最后放回需要的上(下)凸包

以上凸包为例，在获取当前上凸包的所有点数组后，需要获取点pm，使得pm到p1p2的距离最大

将直线方程写成Ax+By+C=0的形式

$$(y_1–y_2)x–(x_1–x_2)y+x_1{y}_2–x_2{y}_1=0$$

点到线距离公式：

$$d=\frac{|Ax+By+c|}{\sqrt{A^2+B^2}}$$

遍历当前点数组，当d最大时，返回点pm

def distance(hull_points: list[list] = [], p1: list = [], p2: list = []) -> list:
    '''计算最远点pm ，返回该点'''
    d = 0
    pm = None
    for p in hull_points:
        if p == p1 or p == p2: continue
        A = p1[1] - p2[1]
        B = p2[0] - p1[0]
        C = p1[0] * p2[1] - p2[0] * p1[1]
        temp = abs(A*p[0]+B*p[1]+C) / math.sqrt(pow(A, 2) + pow(B, 2))
        if temp > d:
            pm = p
            d = temp
    return pm

参数hull_points为当前上(下)凸包中包含的点，p1、p2为当前的两个端点。

到这里并未获得最外层的点，因此需要重复2~3步骤，其中的p1、p2应该变为相应的端点，即每一次的切割凸包都会生成两个子问题，这两个子问题的端点为(p1,pm)和(pm,p2)，典型的分治。

力扣提交完整代码：

def hull(points: list[list] = [], p1: list = [], p2: list = [], isUp: bool = True) -> list[list]:
    '''获取上(下)凸包中的点'''
    hull_points = []
    for p in points:
        x0, y0 = p[0], p[1]
        x1, y1, x2, y2 = p1[0], p1[1], p2[0], p2[1]
        if x1 == x2: continue
        y = (y1-y2)/(x1-x2)*(x0-x1)+y1
        if isUp and y0 >= y:
            hull_points.append(p)
        if not isUp and y0 <= y:
            hull_points.append(p)
    return hull_points

def distance(hull_points: list[list] = [], p1: list = [], p2: list = []) -> list:
    '''计算最远点pm ，返回该点'''
    d = 0
    pm = None
    for p in hull_points:
        if p == p1 or p == p2: continue
        A = p1[1] - p2[1]
        B = p2[0] - p1[0]
        C = p1[0] * p2[1] - p2[0] * p1[1]
        temp = abs(A*p[0]+B*p[1]+C) / math.sqrt(pow(A, 2) + pow(B, 2))
        if temp > d:
            pm = p
            d = temp
    return pm

def convex_hull(ans: list[list] = [], points: list[list] = [], p1: list = [], p2: list = [], isUp: bool = True) -> list[list]:
    '''凸包'''
    hull_points = hull(points, p1, p2, isUp)
    pm = distance(hull_points, p1, p2)
    if pm is not None:
        convex_hull(ans, hull_points, p1, pm, isUp)
        convex_hull(ans, hull_points, pm, p2, isUp)
    else:
        for p in points:
            # 如果 p 在 p1p2 直线上
            if (p2[0]-p1[0])*(p[1]-p1[1]) == (p[0]-p1[0])*(p2[1]-p1[1]):
                if p not in ans:
                    ans.append(p)

class Solution:
    def outerTrees(self, trees: List[List[int]]) -> List[List[int]]:
        trees.sort()
        ans = []
        p1, p2 = trees[0], trees[-1]
        # 上凸包
        convex_hull(ans, trees, p1, p2, True)
        # 下凸包
        convex_hull(ans, trees, p1, p2, False)

        return ans

出现的问题与思考

在获取上(下)凸包中的点的函数hull中有这样一句 if x1 == x2: continue

这里为什么要这么写？不用处理这种情况吗？

因为当两个端点的横坐标相等的时候，斜率公式会报错。（一开始没有注意

这是由于算法一开始取的就是最值端点，若存在若干点在这条直线上，那么会在convex_hull函数中加入最终答案中，因此不需要担心值会缺失。

那么在递归过程中遇到这种情况是否会丢失答案吗？

蒟蒻通过判断pm是否取值为递归判断条件，当递归至pm值不存在时，则表示当前端点上(下)凸包没有值了，那么将这条直线中的所有点(包括端点)加入答案，显而易见，不会导致值缺失。