机器学习
本章节所写笔记,适用于吴恩达机器学习系列课程。
笔记内容大多来源于吴恩达机器学习笔记,不过在学习过程中,会加入自己的理解,以及修改来源中的内容。
监督学习
监督学习指的是,给定的数据集中,每个样本都包含正确‘答案’,算法的目的就是为了给出更多的正确‘答案’。例如预测房价问题,给出了房子的面积和价格;预测肿瘤问题,给出了肿瘤的尺寸和定性。
- 回归问题是预测连续值的输出,例如预测房价。
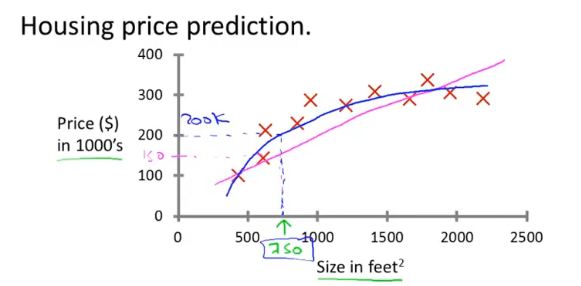
- 分类问题是预测离散值输出,例如判断肿瘤是良性还是恶性。
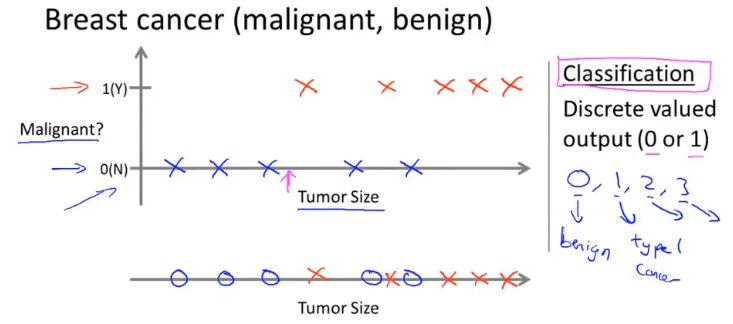
无监督学习
无监督学习是的是,给定的数据集中,不体现/不给定/不知道样本的正确‘答案’,即在没有标签(label)的数据集上进行学习,目的是为了发现数据存在的内在结构。
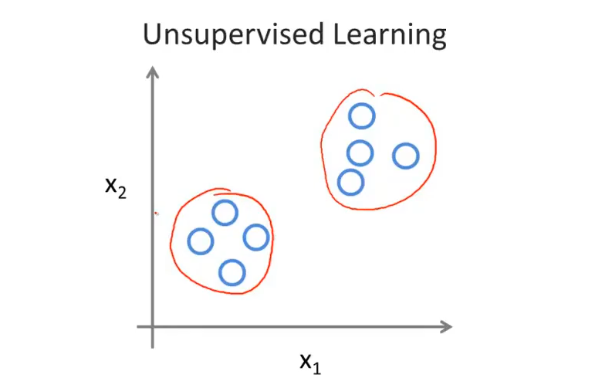
常见的无监督学习任务:
- 聚类(Clustering)
- 降维(Dimensionality Reduction)
- 关联规则学习(Association Rule Learning)
- 密度估计(Density Estimation)
线性回归
线性回归是拟合一条线,将训练数据尽可能分布到线上。另外还有多变量的线性回归称为多元线性回归。
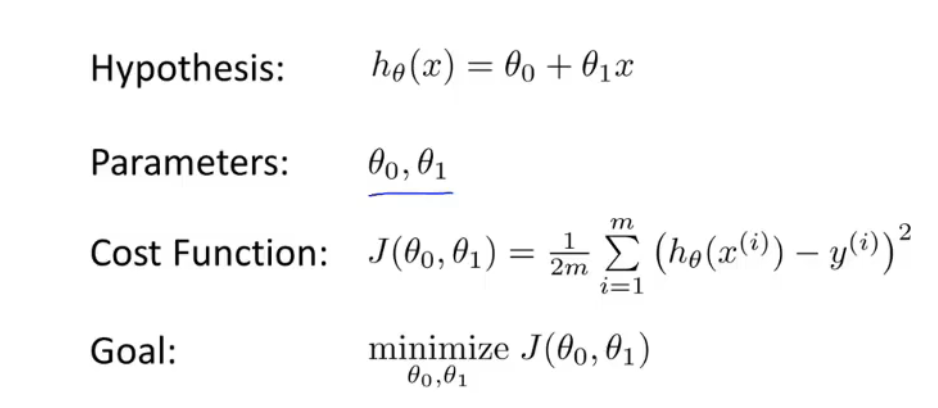
代价函数
代价函数(cost function),一般使用最小均方差来评估参数的好坏。
其中:
- m 表示样本的数量
- h 表示假设函数,通常为:
通过调整θ,使得均方差最小,得到最终的假设函数模型。
梯度下降
首先任意给定参数初值,通过代价函数的梯度,然后不断地调整参数,直到收敛,最终得到一个局部最优解。初值的不同可能会得到两个不同的结果,即梯度下降不一定得到全局最优解。
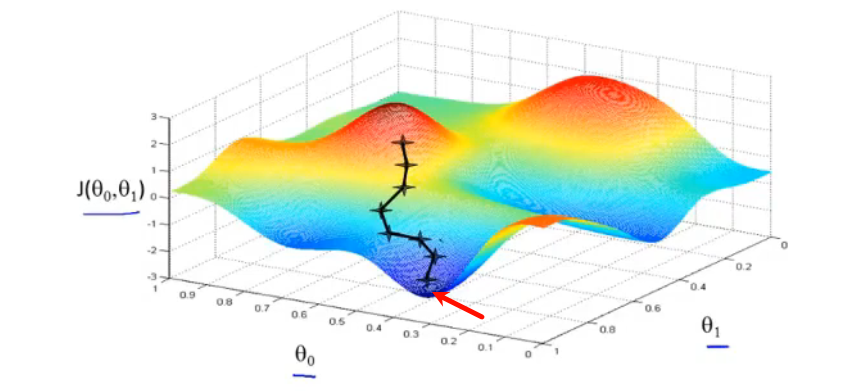
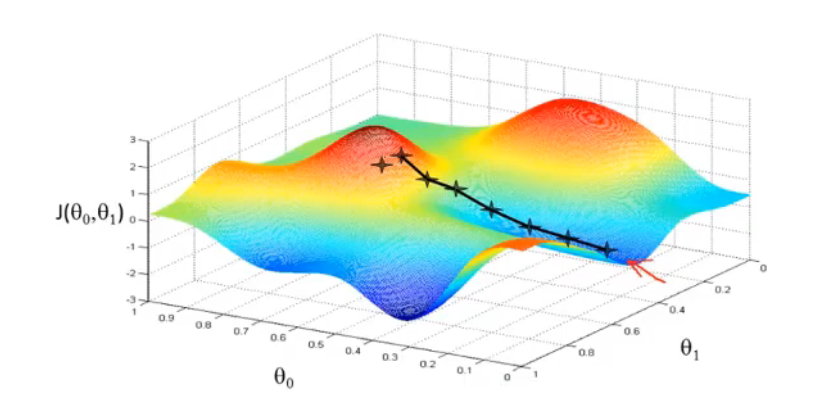
在梯度下降调整参数时,要注意每一次更新需要同时更新所有的参数。

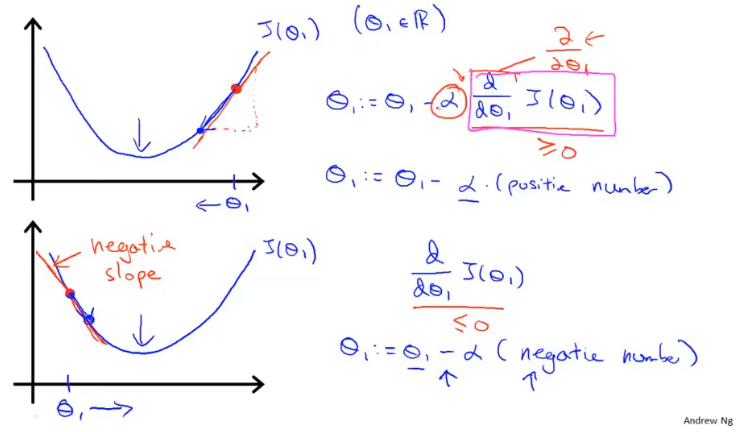
梯度下降公式中有两个部分,其中:
α为学习率,直观的解释为“下山”每一步迈出的步伐大小,即每次参数更新的步长。- 偏导数,用来计算当前参数对应代价函数的斜率,导数为正则减小,导数为负则增大,通过这样的方式可以使代价函数收敛至最低值。
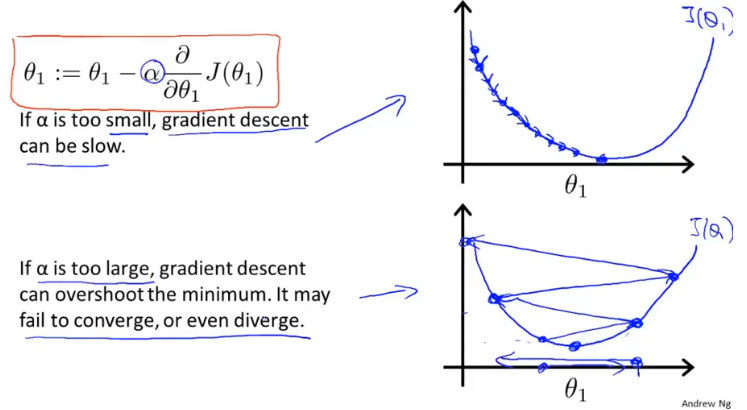
学习率的α大小不好确定,如果太小则需要很多步才能收敛,如果太大最后可能不会收敛甚至可能发散。
当θ处于局部最优解时,θ的值将不再更新,因为偏导为0。
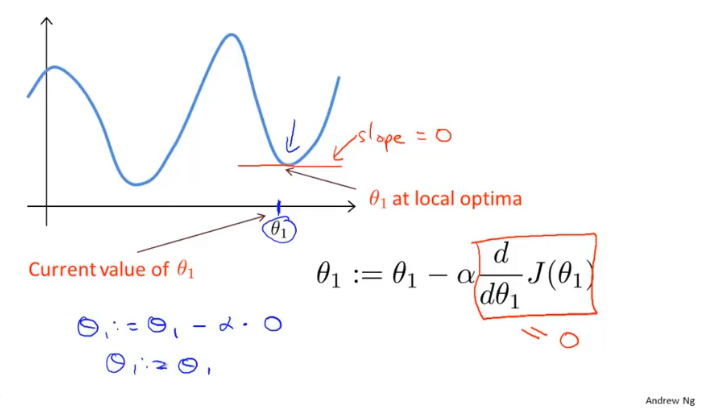
这也说明了即使学习率α不改变,参数也可能收敛,假设偏导>0,因为偏导一直在向在减小,所以每次的步长也会慢慢减小,所以α不需要额外的减小。
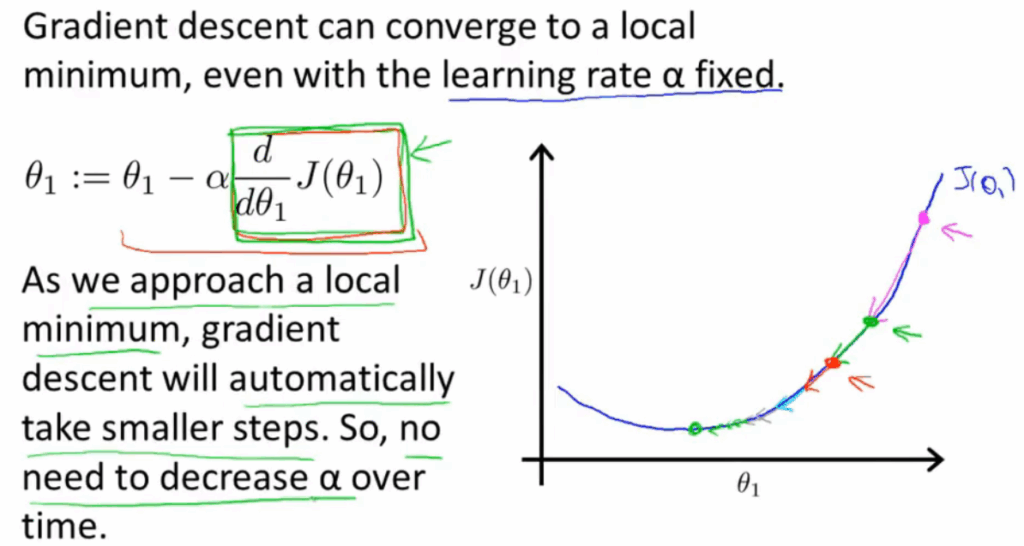
单元梯度下降
梯度下降每次更新的都需要进行偏导计算,这个偏导对应线性回归的代价函数。

对代价函数求偏导的结果为:
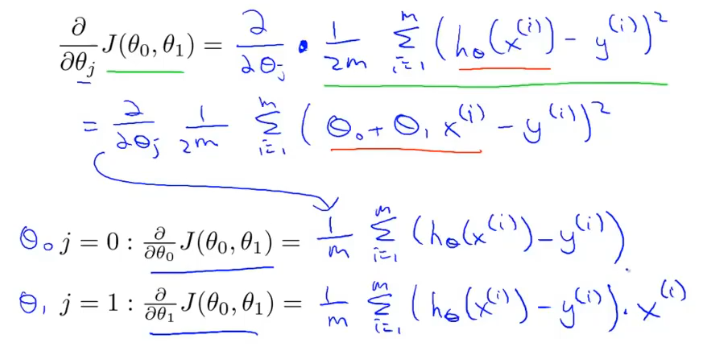
梯度下降的过程容易出现局部最优解,不过线性回归的代价函数通常是凸函数,因此总能收敛到全局最优。
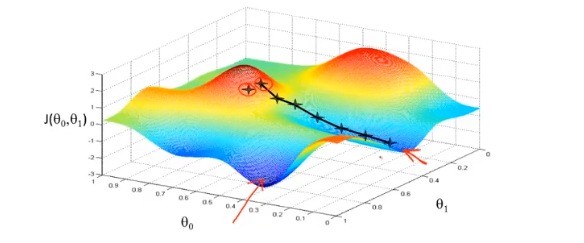
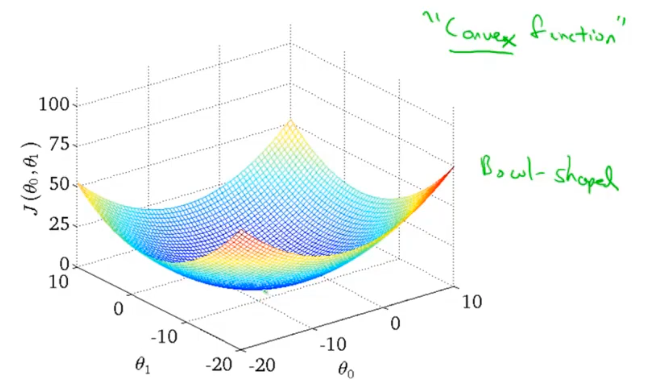
梯度下降过程的动图展示:
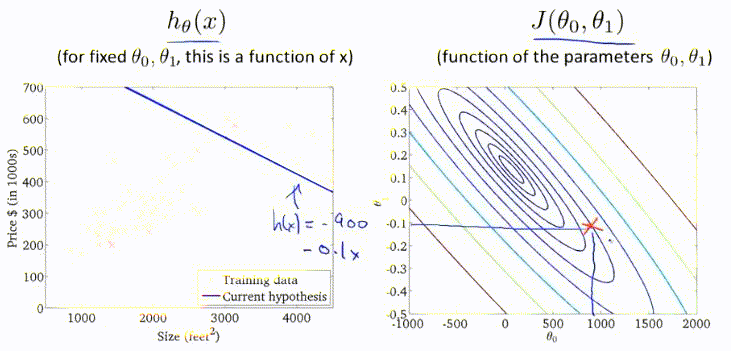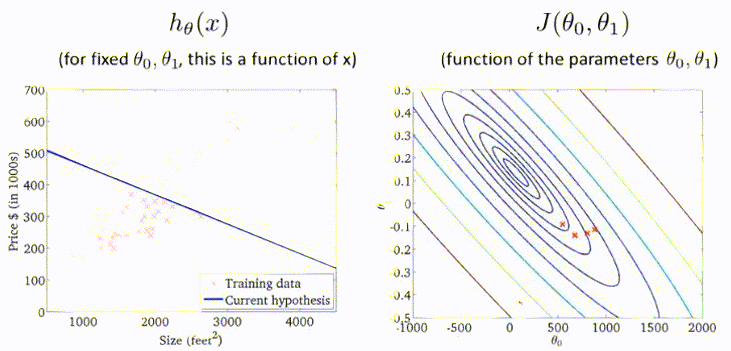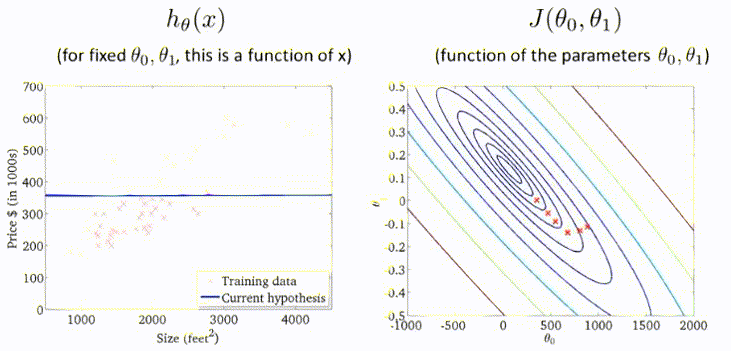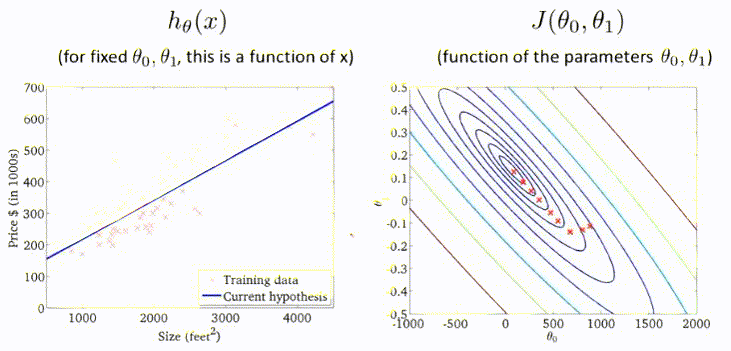
以上介绍的梯度下降方法有时也称为Batch Gradient Descent,即批量梯度下降。这意味着每一步梯度下降,都需要遍历整个训练集的样本。效果虽然显著,但是效率低。
矩阵和向量
一些数学计算转化为矩阵的形式,可以简化代码书写、提高效率、代码更容易理解。
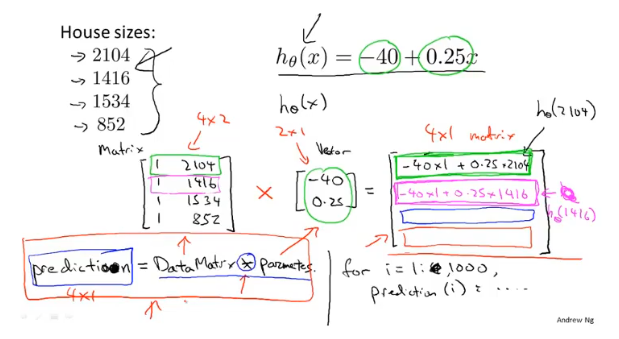
例如下图计算,根据假设函数的形式,初始化矩阵第一列为1,对应常数θ_0。图二中3个假设函数组成一个2×3的矩阵/3个二维向量组,一步矩阵运算即可得到很多结果。
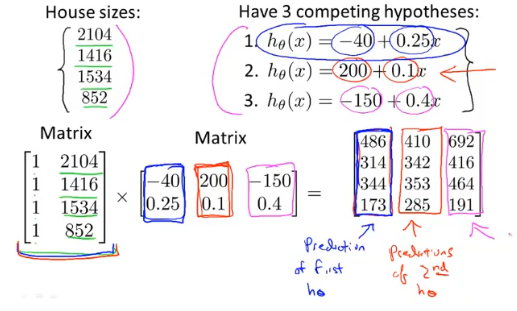
多元梯度下降
通常问题都会涉及到多个变量,例如房屋价格预测就包括,面积、房间个数、楼层、价格等
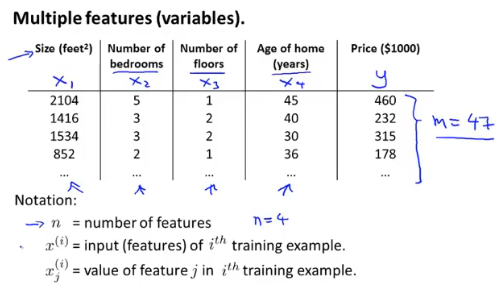
因此代价函数就不再只包含一个变量,为了统一可以对常量引入x0=1变量
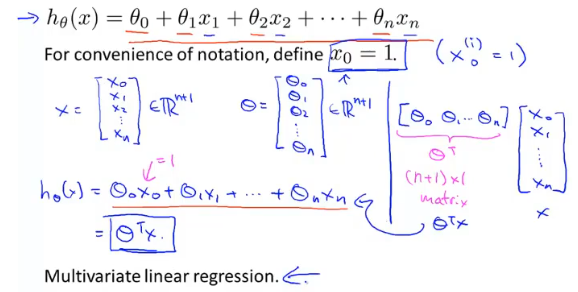
虽然参数的个数增多,但是对每个参数求偏导时和单个参数类似。

由图可知,θj有通式:
且不难发现n=1与n≥1的θ0本质是一样的,因为我们通常定义xi0=1
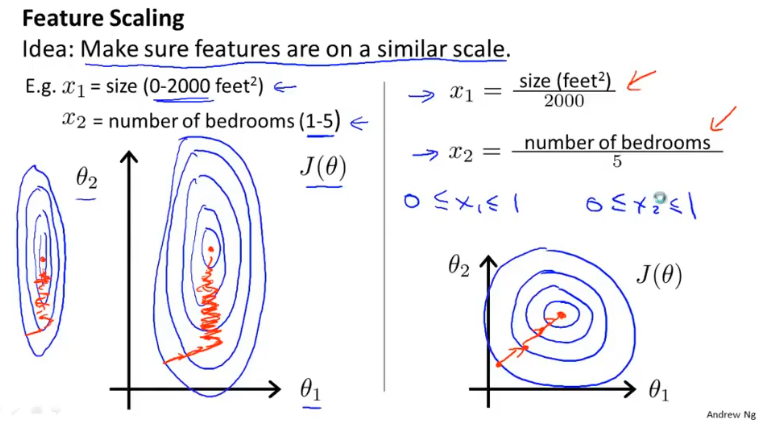
特征缩放
特征值缩放的目的是为了加速梯度下降。多个变量的度量不同,数字之间相差的大小也不同,如果可以将所有的特征变量缩放到大致相同范围,这样会减少梯度算法的迭代。
特征缩放不一定非要落到[-1,1]之间,只要数据足够接近就可以。
其中:
μ表示平均值σ表示标准差,方便点也可以使用定义域范围S


学习率
学习率α的大小会影响梯度算法的执行,太大可能会导致算法不收敛,太小会增加迭代的次数。
为了减少迭代次数,我们通常会选取一个阈值ε来表示近似0。

不过还可以画出每次迭代的J(θ)的变化,来判断当前算法执行的情况,然后选择合适的学习率。
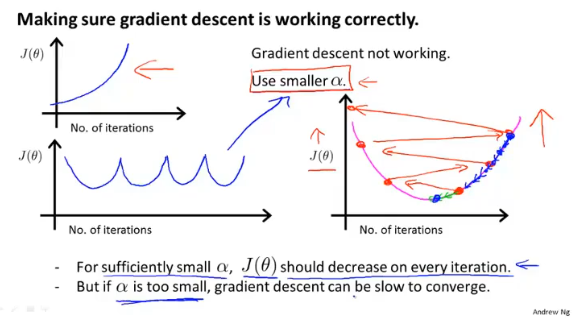

总的来说:
- 当
iteration-J(θ)曲线不是都下降时,调低学习率α - 当梯度下降过慢时,调高学习率
α
多项式回归
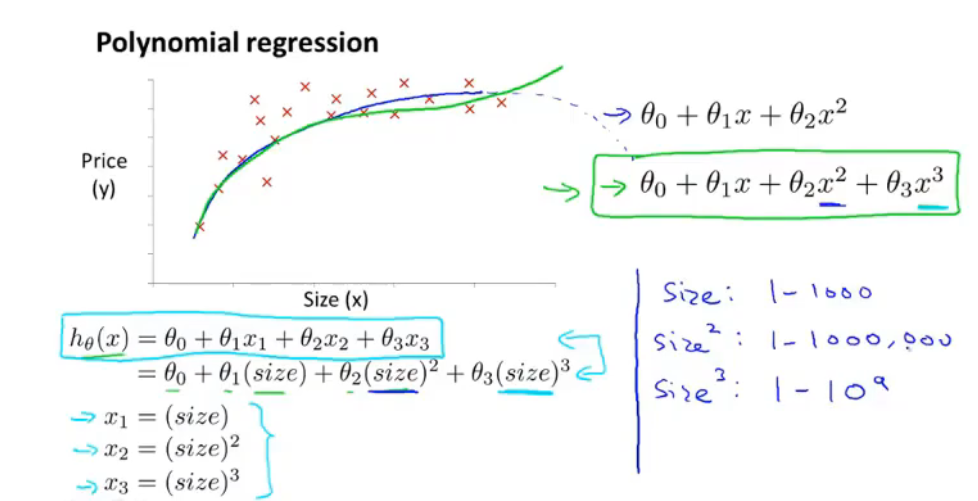
当一个模型有两个或多个特征时,有时可以将其合并成一个特征,例如房屋的占地面积:
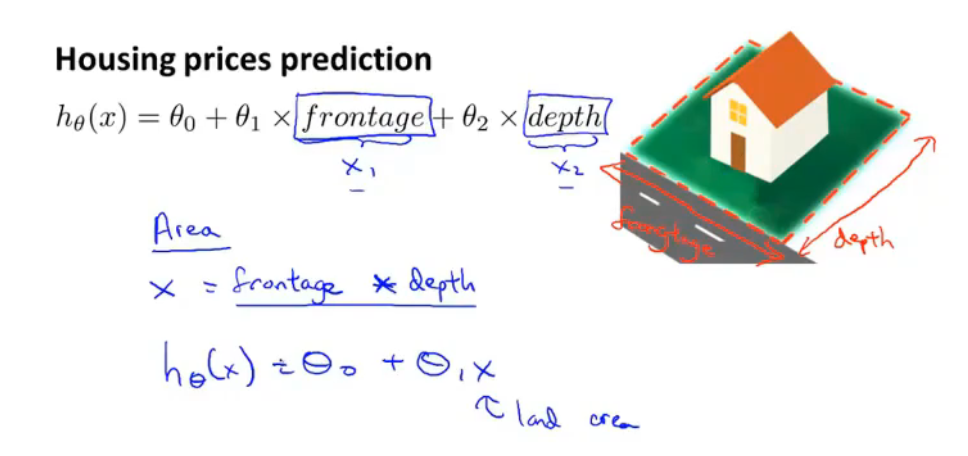
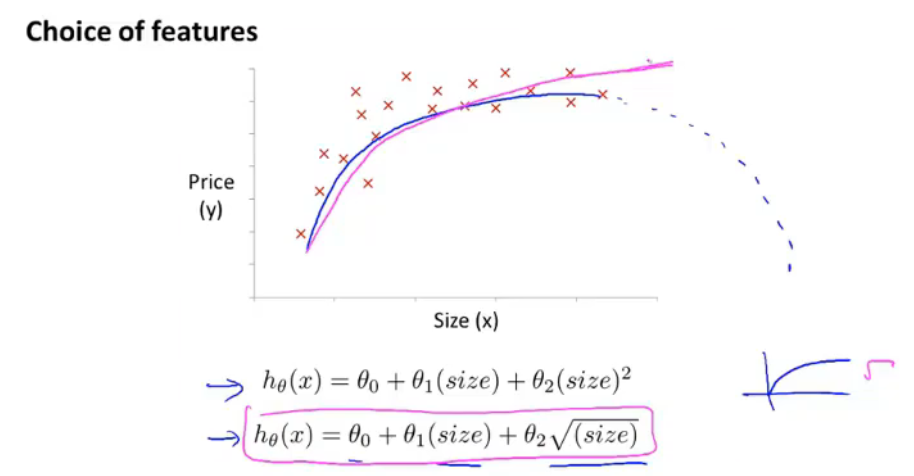
当假设函数的多项式不能满足预测模型时,可以调整多项式的种类,例如:
正规方程
用于线性回归中直接计算最优参数θ的解析解:
利用线性代数的方法直接求解θ。
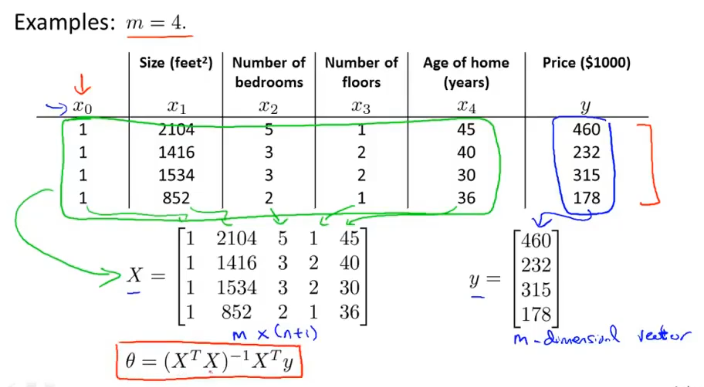
θ的推导是根据等式XΘ=y得到的,XTX的目的是将矩阵转化为方阵,因为求矩阵的逆的前提是方阵。
矩阵可能存在不可逆的情况,例如特征之间存在相关性、样本数量≤特征数量。
这时可以删除一些不必要的特征,或使用正则化。
梯度下降和正规方程的优缺点

逻辑回归
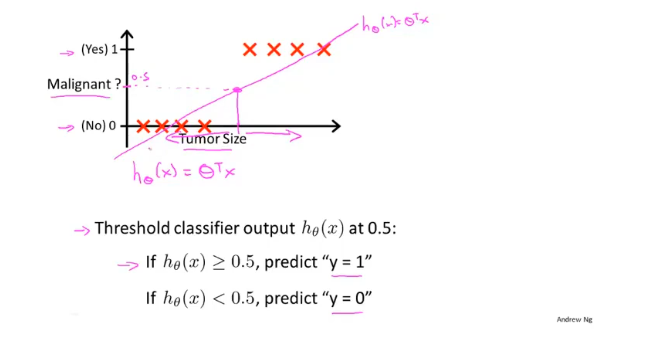
逻辑回归(Logistic Regression)用于解决分类的问题,如果使用线性回归可能会造成很大的误差;假如样本的标签值为0、1,线性回归输出值是连续的,存在>1和<0的情况,不符合实际。
如果对于一个均匀的数据,使用线性回归,选取0.5作为分界线,可能会得到一个比较准确的模型,但是如果数据不太均匀就会存在很大的误差。
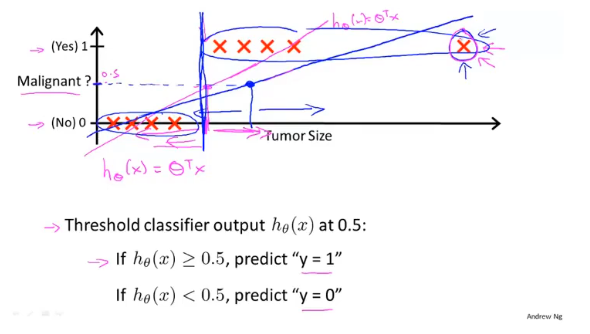
激活/逻辑函数
Sigmoid/Logistic function
sigmoid函数:
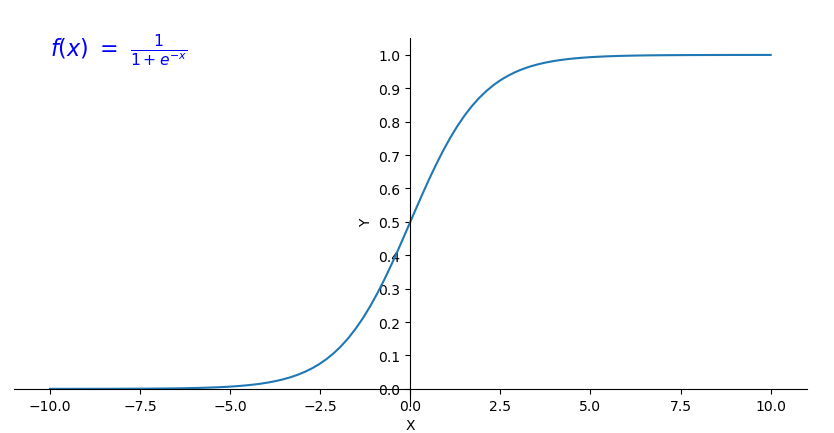
激活函数的y值分布在[0,1]内,对于分类问题,我们可以使用激活函数的值来表示满足特征的概率。

决策边界
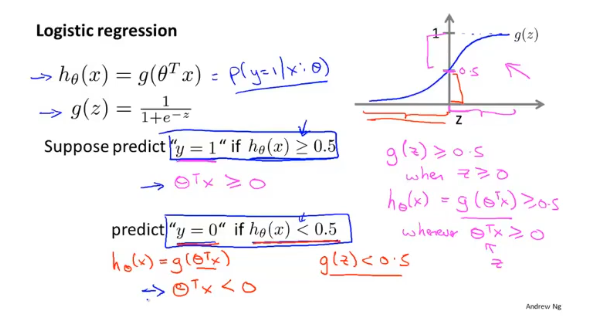
决策边界是假设函数的一个属性,取决于函数的参数,而不是数据集。
假设以x=0,y=0.5作为判断的界限,当θTx≥0.5,预测y=1;θTx<0.5,预测y=0。
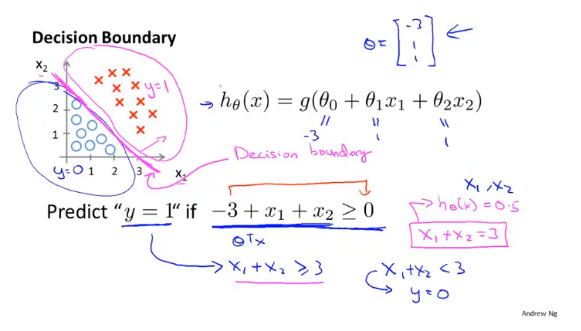

简言之,就是令假设函数为0即可求出决策边界。
代价函数
对于sigmoid函数,如果使用类似线性回归的代价函数cost=Σ(h(x)-y)2,将得到一个非凸函数(图左),这样就不能使用梯度下降的方法求解全局最优解。因此应该另寻它路,寻找其它的代价函数。
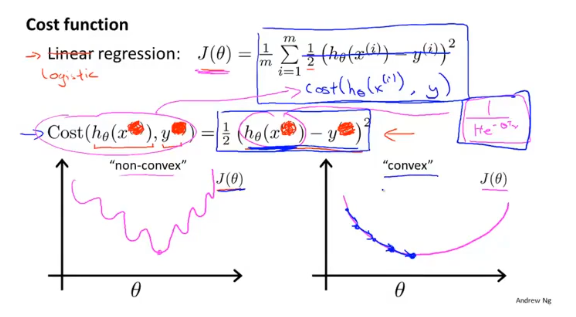
逻辑回归一般使用对数函数作为代价函数:
首先对于分类函数来说,它的假设函数hθ(x)输出值范围为[0,1],得到的对数图像如下:
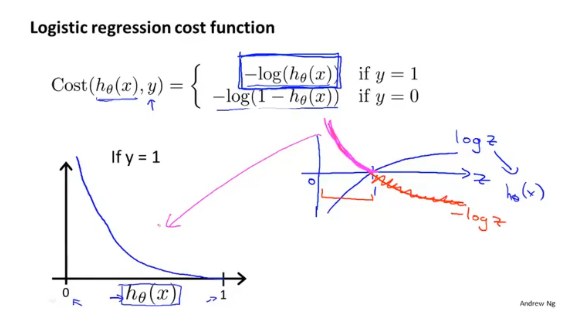
当评估模型参数对y=1(恶性肿瘤)进行预测的好坏时,如果实际为恶性,预测值也为1(恶性),此时的代价为0;如果实际为恶性,预测为0(良性),此时的代价为+∞(模型惩罚非常大),这时代价函数就很好的评估了参数θ的表现。
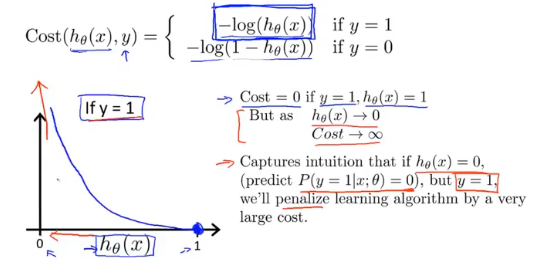
同样对于y=0(良性肿瘤)的代价函数为:
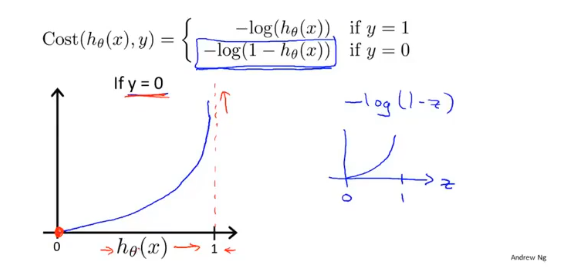
由于y的取值只有0、1,可以将上面两个函数合并,评估当前参数的代价J(θ)为:

即代价函数cost=
梯度下降
在确定代价函数之后的任务是,如何最小化代价函数,因为代价函数是凸的,所以可以使用梯度下降求解。


虽然求偏导之后,更新θ的形式和线性回归类似,但是它们本质不同,因为hθ(x)不再是简单的线性函数。

多元分类
以三元举例。要解决三元分类问题,首先将其分成三组分别计算决策边界:
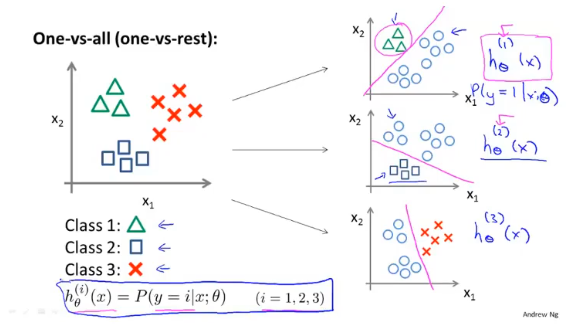
对每个特征单独训练,在做预测的时候,取三个分类器结果最大的。

过拟合
模型对于训练集有着很好的理解,表现为代价函数近似于0,但是对于新数据的预测不是很准确。造成过拟合的原因有多种,特征多且训练集小、假设函数不合理。
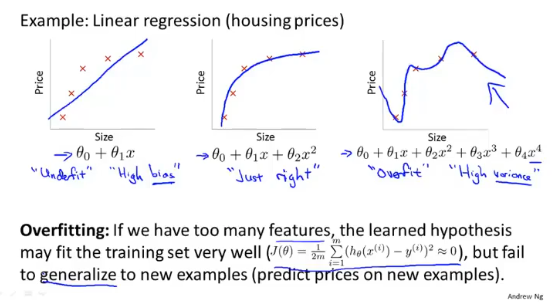
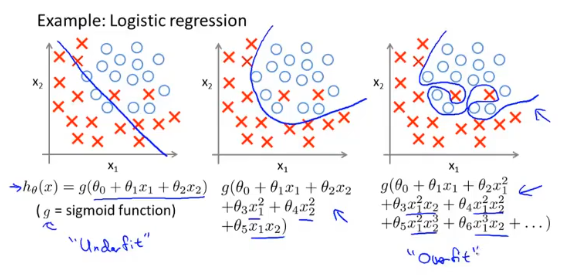
为了避免过拟合,一般采用以下两种方式:
- 减少特征
- 正则化

正则化
多项式的假设函数中,高阶匹配的θ值越大越容易出现过拟合的现象。因此在代价函数中加入正则项,通过λ的值来平衡拟合程度和参数的大小。
例如在预测房价模型中,要是的高阶多项式类似二次一样平缓,要做的就是减小高阶参数的常数项θ,使假设模型近似二项式。
值得注意的是,正则项中,λ对于θ的惩罚是从θ1开始的。
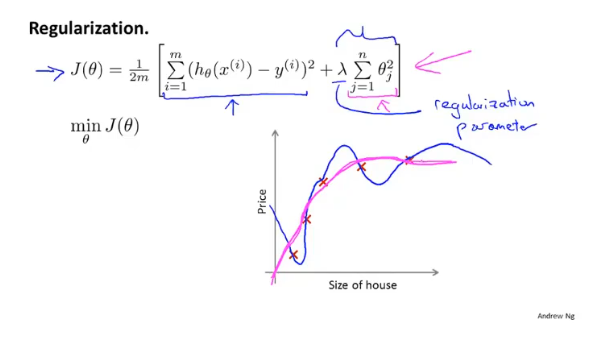
如果λ过大,导致θ≈0,那么最终只剩下θ0,图像将变成一个直线。

线性回归的正则化
梯度下降
代价函数中添加了正则项,因此θ1开始的更新也随之发生变化。

直观的看,正则化导致的变化在于先将每次的θ都减小一点点后,再更新。
正规方程
正规方程的正则化不仅优化了模型,当还λ>0时,有效地解决了XTX可能不可逆的问题。
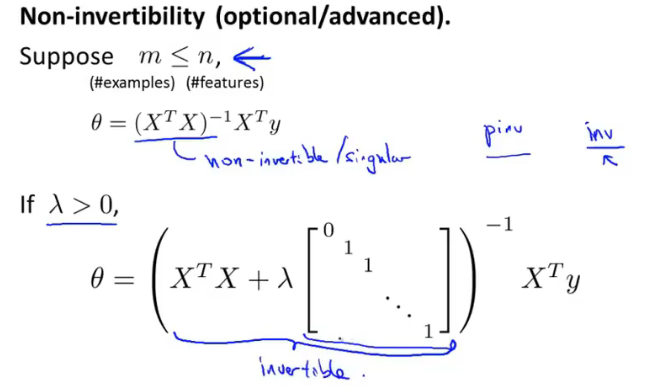
逻辑回归的正则化
与线性回归一样,逻辑回归的代价函数中也需要加上正则项:
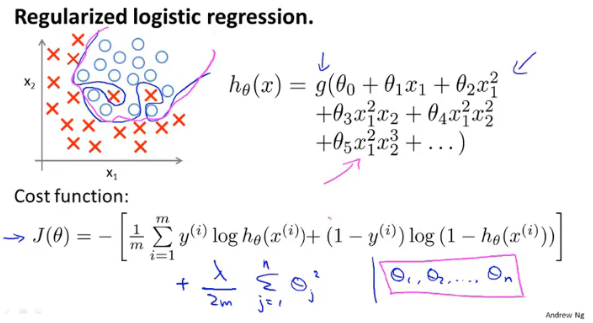
梯度下降
代价函数中添加了正则项,因此θ1开始的更新也随之发生变化。

神经网络
大多数的机器学习所涉及到的特征非常多,对于非线性分类问题,往往需要构造多项式来表示数据之间的关系,多项式的组成方式千变万化,这对计算带来一定困扰。
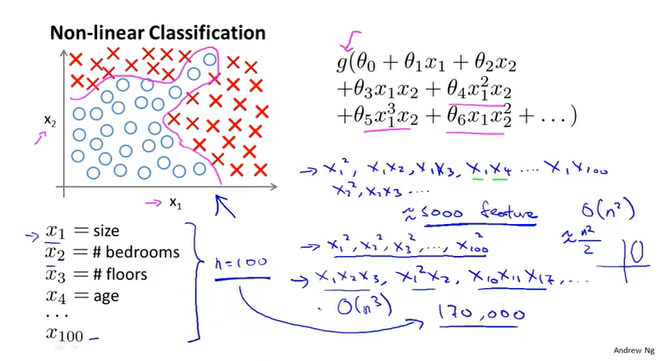
机器学习中的神经网络一般包括三部分,输入层,隐藏层,输出层。其中,隐藏层可以不止一个。
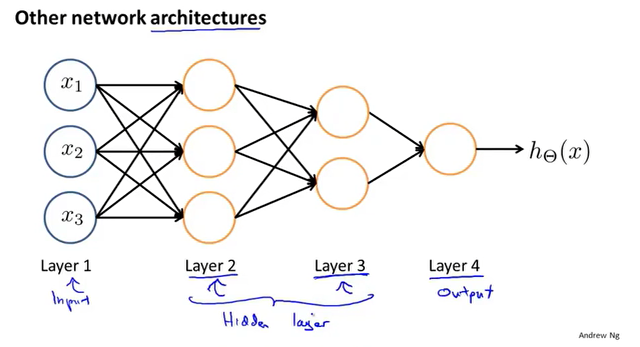
由下图,不难发现,最后一个隐藏层到输出层的本质是逻辑回归运算。
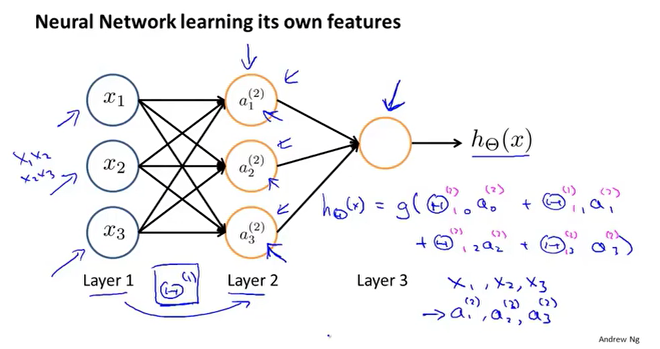
输入层=>隐藏层1=>隐藏层2=>……=>输出层,每一次的运算叫做向前传播,下一层的输入为上一层的输出,并且下一层的值需通过激活函数。
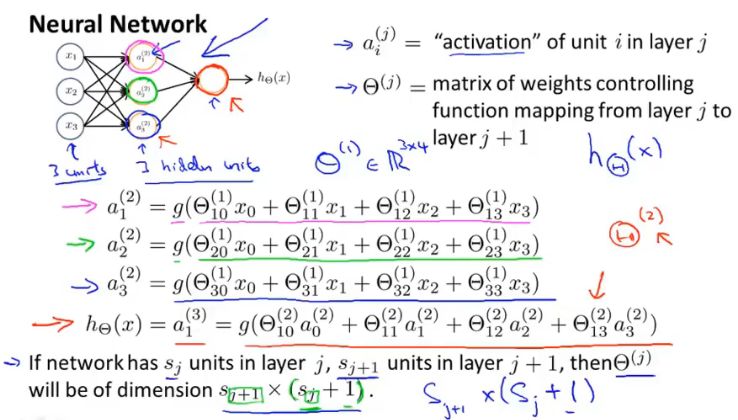
逻辑运算
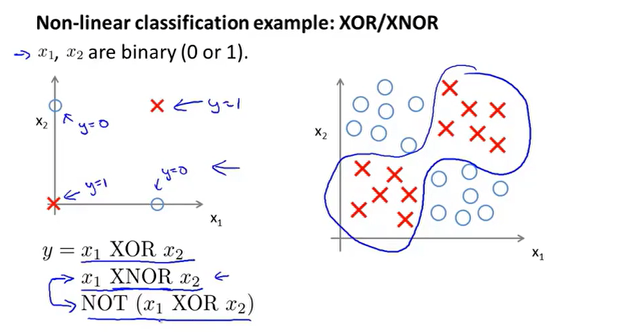
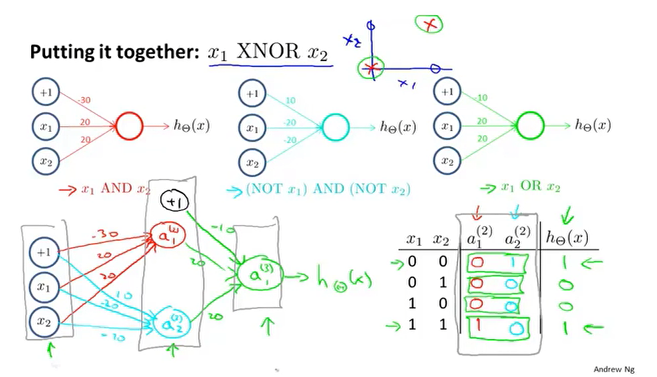
如上为一个XNOR的分类问题,Misplaced &
我们可以先搭建出每种逻辑运算的神经网络,最终整合得到XNOR的神经网络模型。
AND运算
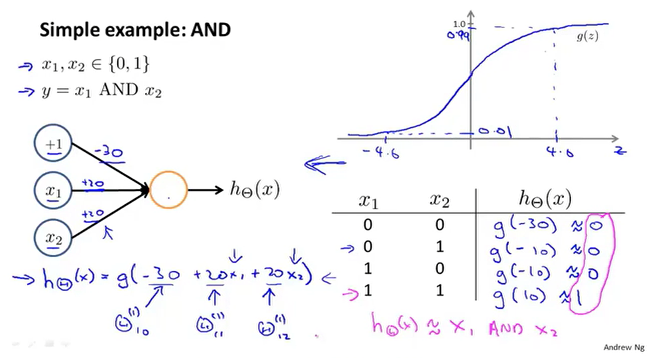
OR运算

NOT运算
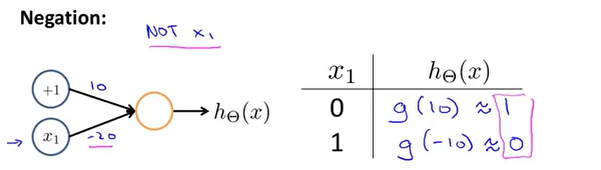
XNOR运算
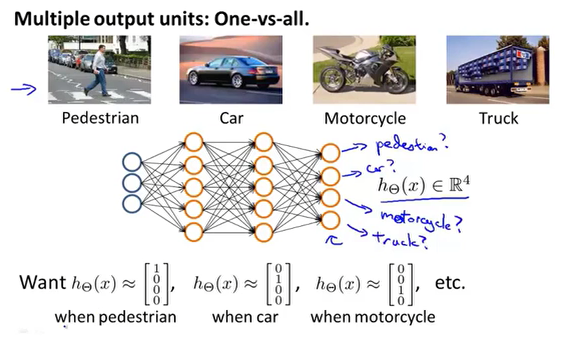
多元分类
通过构建神经网络,输出层的结果为n维,对应n个分类元素。
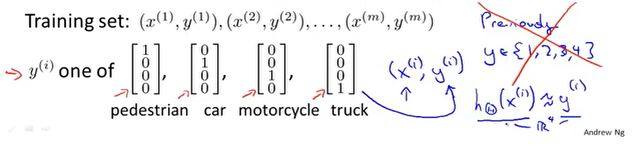
代价函数

其中K表示输出层的单元数目,即有K个元素需要分类。
向前传播
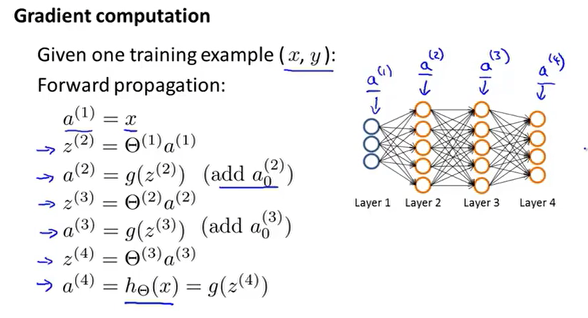
反向传播
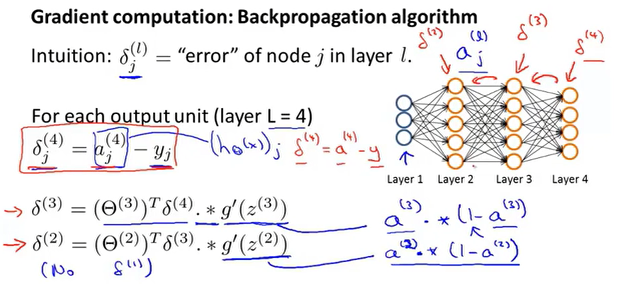

参数/权重的更新
参数的更新其实是正向传播与方向传播的交替运行。
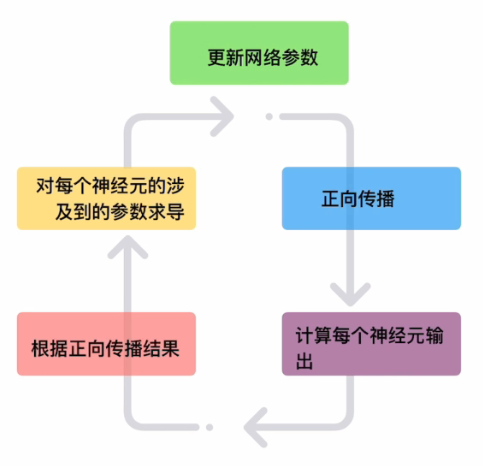
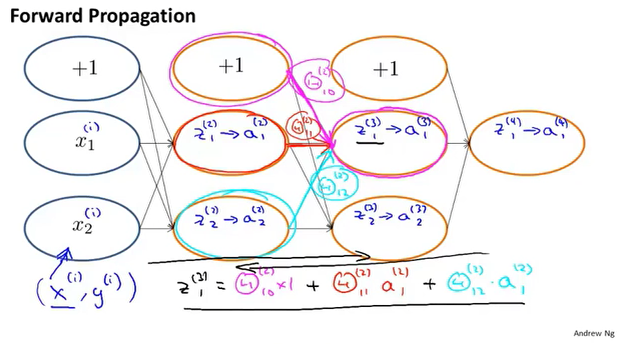
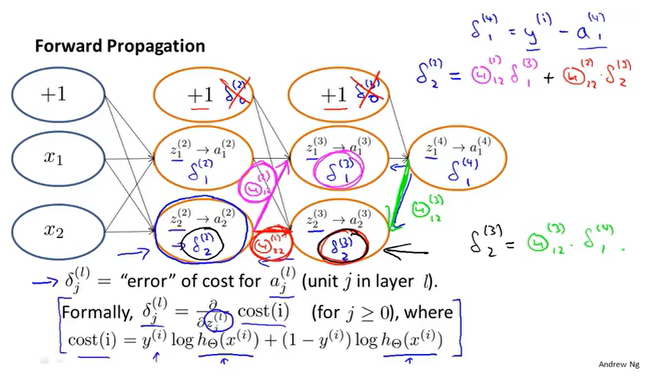
梯度检测
在实现反向传播算法时,如何确保梯度计算正确呢?
在数学上可以使用拉格朗日中值定理来近似的表示曲线上某一点的导数,梯度检测正是使用的这种思想。
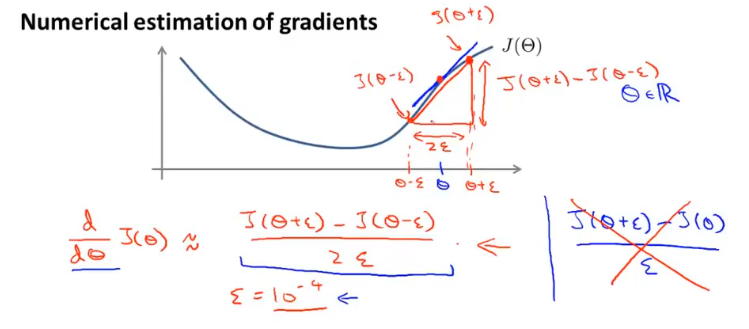
对于n维的参数,梯度检测的使用,可以对每个参数单独进行验证。

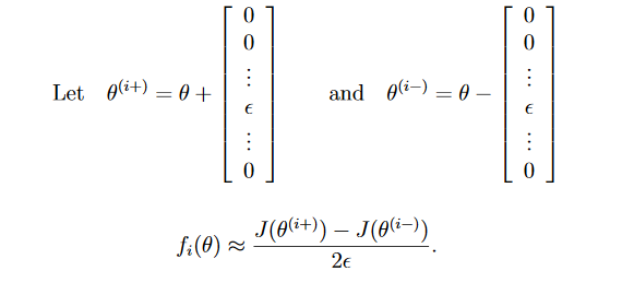
假设通过中值定理得到的梯度为approx_grad,经过反向传播得到的梯度为grad,如果满足以下等式,则说明反向传播得到的梯度精度还行。
由于梯度检测特别耗时,因此在检测算法无误后,训练学习时需要关闭检测。

随机初始化
在对神经网络进行训练时,theta的取值要随机取值,如果都赋值为0,就会使得每一层的输出值、误差相同,从而存在大量冗余。
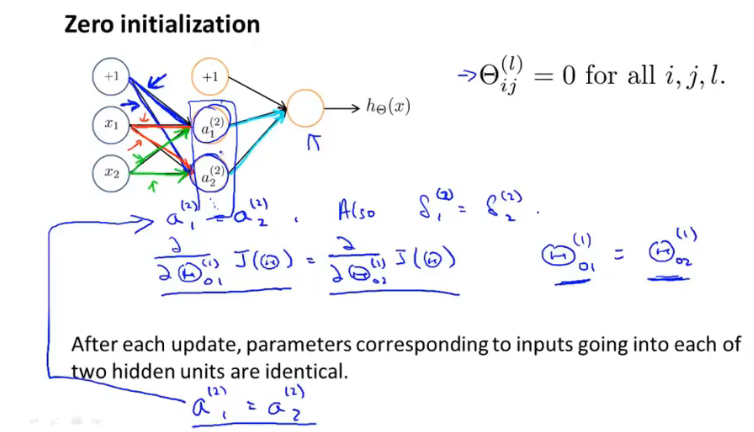
模型评估
训练集&&测试集
在训练模型时,应把收集来的数据集按照7:3的比例拆分为训练集和测试集。训练集得到参数θ,然后使用测试集的数据对参数进行评估,即计算误差。
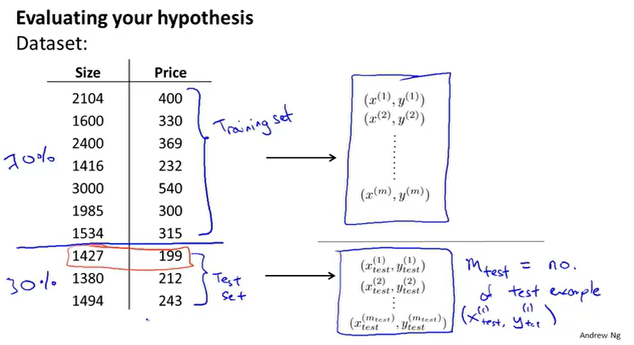
误差计算
线性回归模型的评估

逻辑回归模型的评估

训练集&&验证集&&测试集
将数据集直接分成训练集和测试集,通常情况下可以获得不错的结果。
但是这样做并不能评估模型的泛化能力,通过测试集评估选择的模型,可能刚好适合测试集的数据,并不能说明它对其他数据的预测能力,这时就引入了验证集。验证集=>交叉验证(cross validation, cv)

将数据集按照比例6:2:2拆分为训练集、验证集以及测试集,当然拆分比例可以适当调整。
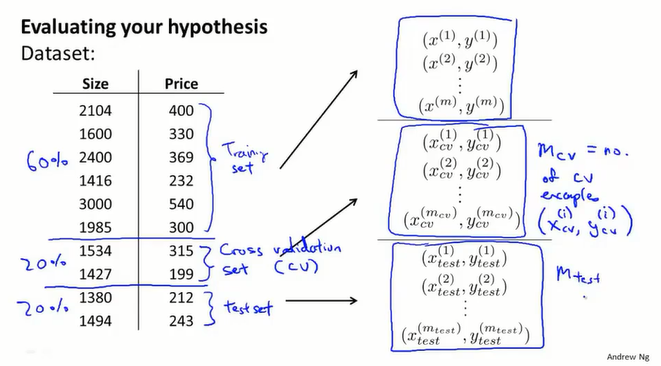
计算每个集合的误差:

这样在选择模型的时候,可以先使用训练集得到每个模型的θ,然后使用验证集评估得到误差最小的模型,最后使用测试集评估他的泛化能力。

偏差&&方差
当假设函数多项式次数增大时,训练集的误差慢慢减小,因为多项式次数越高,图像拟合的就越准确。但是验证集不同,它的趋势是先减少后增大,这分别对应着欠拟合和过拟合。
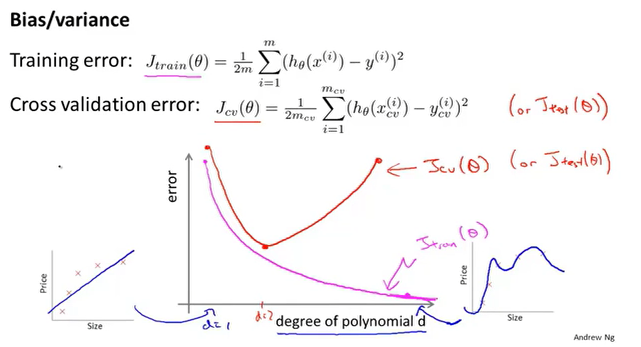
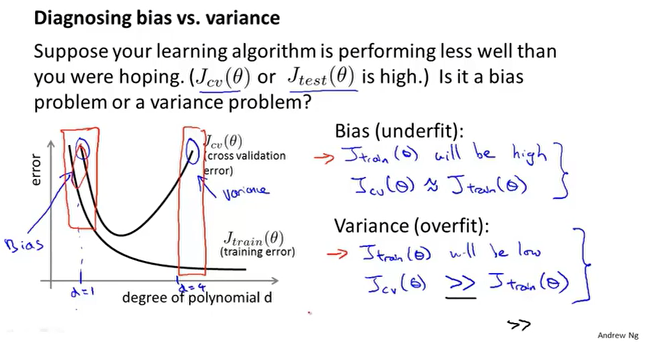
那么我们可以根据误差的不同表现来区分偏差和方差。
- 高偏差(欠拟合):训练误差和验证误差都很大。
- 高方差(过拟合):训练误差小,验证误差大。
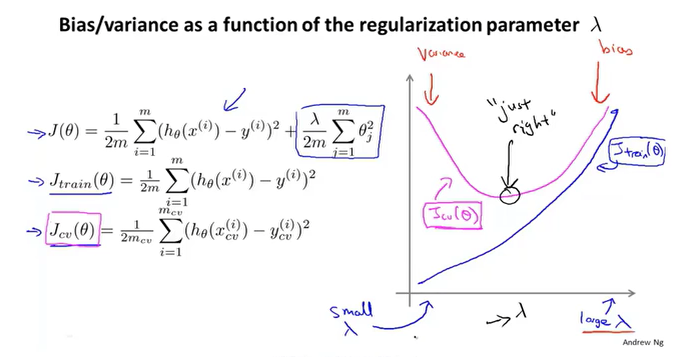
正则化与偏差&&方差
正则项参数λ的取值影响模型的偏差和方差。
λ很大 => 高偏差(欠拟合),模型偏差大,交叉验证误差大λ很小 => 高方差(过拟合),模型偏差小,交叉验证误差大
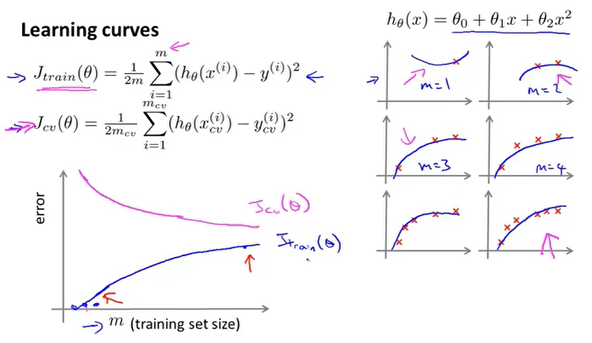
学习曲线
我们通过绘制m-error图像来直观的观察样本数量对于模型学习质量的影响。
假设模型不变,随着数据量的增加,训练的代价函数的误差慢慢增大,因为数据越多,模型越不容易拟合;交叉验证的误差慢慢减少,因为数据越多,模型越精准。
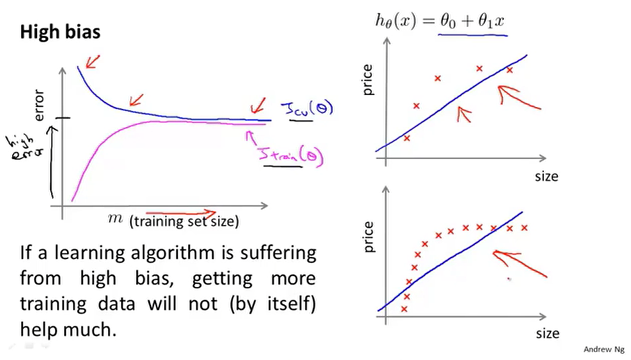
高偏差的学习曲线
因为参数少,数据多,所以随着数据量的增多,高偏差模型的训练代价和交叉验证代价会很接近,甚至趋于水平。这时选择增加数据就不是很好的选择了,可以尝试增加数据的特征。
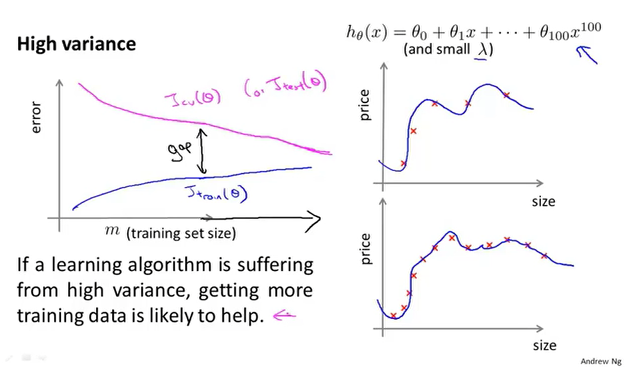
高方差的学习曲线
高方差的特点是训练误差和验证误差之间有很大的差距,这是因为特征多导致的过拟合。这时可以选择增加数据,随着图像右移可以看出训练误差和验证误差会慢慢接近。
调试算法
绘制学习曲线,找到问题是高偏差还是高方差。
高偏差:
- 增加特征
- 增加多项式特征(
x12,x1x2) - 减小正则参数
λ
高方差:
- 减少特征
- 减少多项式特征(
x12,x1x2) - 增大正则参数
λ
系统设计
在设计一个神经网络时,首要的任务就是0->1,先简单的实现训练、交叉验证以及测试。随后绘制学习曲线,查看模型是否存在高偏差/高方差的问题,做相应的调试。
除了观察学习曲线以外,还应该不断的留意交叉验证的误差,找到问题的根本,这就是误差分析。
误差分析
以邮箱分类举例,算法错误的分类了100封邮件,我们应对这个错误进行人工分析,纠正/完善算法。
上文提到的要找到问题的根本,在这个例子中,问题的根本可以缩小为:
- 错误分类的100封邮件中最多的邮件类型,对它们进行误差分析
- 导致错误分类的最多的特征/因素,对它们进行误差分析

在完善算法的过程中,应设置对照组,通过交叉验证的结果判断优化的方向是否正确。
不对称性分类的误差分析
何为不对称性分类?例如对癌症的预测,相对于样本数据真实得癌症的人非常少,大概只有0.5%的概率,这样的问题称为偏斜类/不对称性分类,一个类中的样本数比另一个类多得多。
假设分类中标签为0的类占比仅有5%甚至更少,那么只输出y=1的函数都比你的模型准确。对于偏斜类的问题,如何评估模型的精准度呢?
这里引入查准率和召回率这两个概念。
查准率、召回率
查准率 = 真 真值 / 预测真值
召回率 = 真 真值 / 标签真值
其中 <真 真值> 指的是 <预测真值>∩<标签真值>
对于偏斜分类的样本:
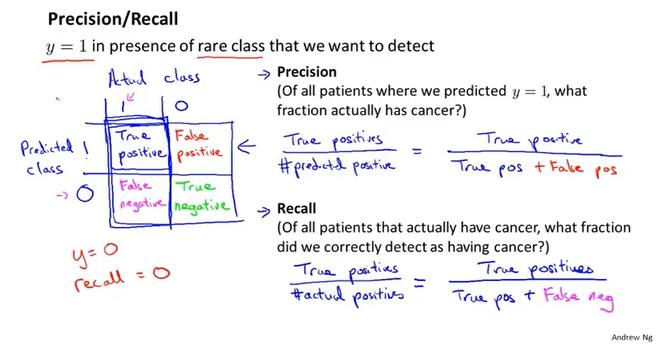
当查准率和召回率足够高时,可以对于这个偏斜分类来说,我们的算法表现的很好。但是这两个值通常不可兼得,因此我们需要根据需要进行调整。

通常,我们可以调整预测的临界值来调整查准率和召回率:
- 阈值设置的高,那么对应的查准率高、召回率低
- 阈值设置的低,那么对应的查准率低、召回率高
那么,应该如何通过这两个值的大小来判断哪个算法更优呢?下面引入F score这个概念。
F1 score
F1score,即调和平均数(倒数的平均数)
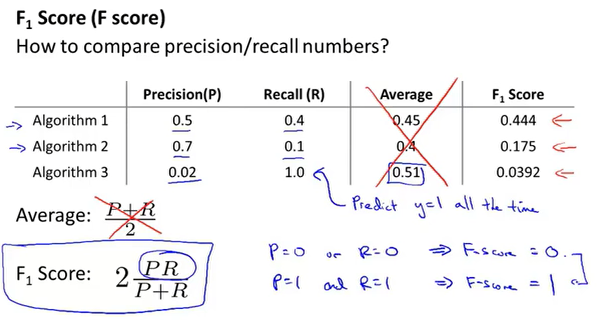
F1score会比较照顾数值小的一方,如果PR都为0,F1score=0;如果PR都为1,F1score=1
作业
线性回归梯度下降
数据处理:
data_path = 'ex1data2.txt'
data = data = pd.read_csv(data_path, names=['Size', 'Rooms', 'Price'], dtype=float)
data.insert(0, 'Ones', 1) # 在第一列插入全为1的列
columns = data.shape[1]
X = data.iloc[:,:columns-1]
y = data.iloc[:,columns-1:columns]
# 将数据转换为矩阵形式
X = np.asmatrix(X.values)
y = np.asmatrix(y.values)
theta = theta = np.asmatrix(np.zeros((1, columns-1)))代价函数:
def cost_cal(X, y, theta):
inner = np.power(X * theta.T - y, 2)
return np.sum(inner, axis=0) / (2 * X.shape[0])梯度下降:
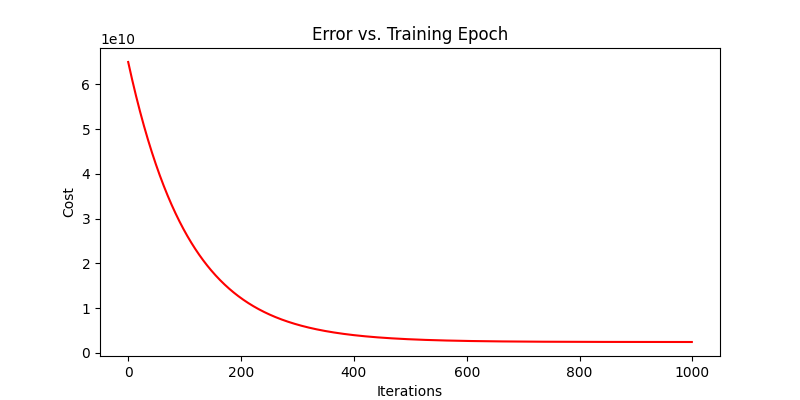
def gradient_descent(X, y, theta, rate, epoch):
m = len(X) # 样本数量
cost = np.zeros(epoch) # 初始化一个ndarray,包含每次epoch的cost
for i in range(epoch):
# 计算梯度
theta = theta - (rate / m) * (X * theta.T - y).T * X
# 计算结果一致,为了看的明白可以这样写
# error = X * theta.T - y # (m x 1)
# grad = (X.T * error) / m # (n x 1)
# theta = theta - rate * grad.T # (1 x n)
cost[i] = cost_cal(X, y, theta).item() # 计算当前的cost
return theta, cost学习率α= 0.000000001,结果:
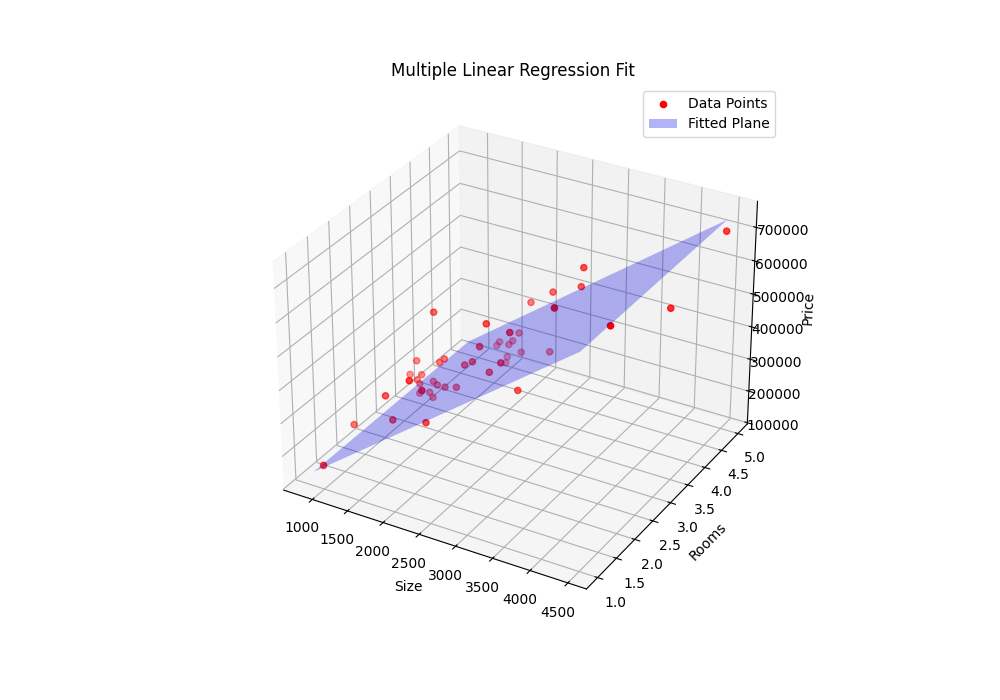
正规方程
线性回归的代价函数是凸函数,此时可以使用正规方程快速求解。而逻辑回归代价函数是非线性的,因此没有解析解。
正规方程:
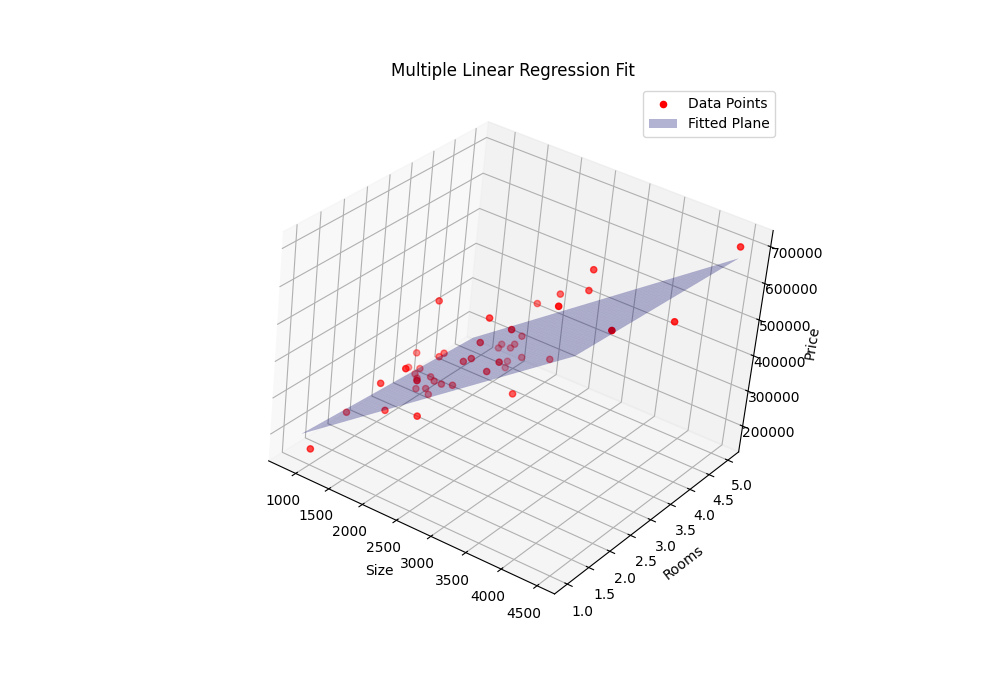
def normal_equation(X, y):
theta = np.linalg.inv((X.T @ X)) @ X.T @ y
return theta结果:
逻辑回归梯度下降
sigmoid函数:
def sigmoid(z):
return 1 / (1 + np.exp(-z))代价函数:
def cost_logi_cal(X, y, theta):
m = X.shape[0]
h = sigmoid(X @ theta.T)
cost = -1 / m * (np.sum(y.T @ np.log(h) + (1 - y).T @ np.log(1 - h)))
return cost梯度下降:
def gradient_descent_logi(X, y, theta, rate, epoch):
m = X.shape[0]
cost = np.zeros(epoch)
for i in range(epoch):
theta = theta - (rate / m) * ((sigmoid(X @ theta.T) - y).T @ X)
# 逐步解析
# h = sigmoid(X @ theta.T) # 预测值 (m x 1)
# error = h - y # (m x 1)
# grad = (X.T @ error) / m # (n x 1)
# theta = theta - rate * grad.T # (1 x n)
cost[i] = cost_logi_cal(X, y, theta)
return theta, cost数据读取与处理:
# 数据读取
data_path = "ex2data1.txt"
data_raw = pd.read_csv(data_path, names=['Exam1', 'Exam2', 'Admitted'])
# 数据处理
data = data_raw.copy()
# 归一化特征
# 计算标准化所需参数
mean = data_raw[['Exam1', 'Exam2']].mean()
std = data_raw[['Exam1', 'Exam2']].std()
data[['Exam1', 'Exam2']] = (data[['Exam1', 'Exam2']] - mean) / std
data.insert(0, 'ones', 1)
columns = data.shape[1]
X = data.iloc[:, : columns-1]
y = data.iloc[:, columns-1: columns]
学习率α= 0.1结果:
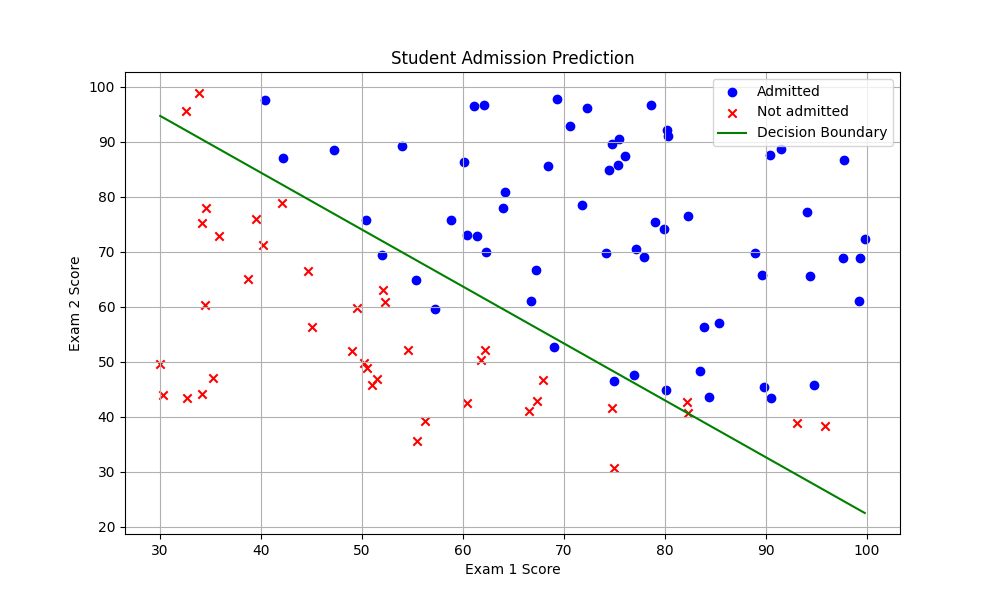
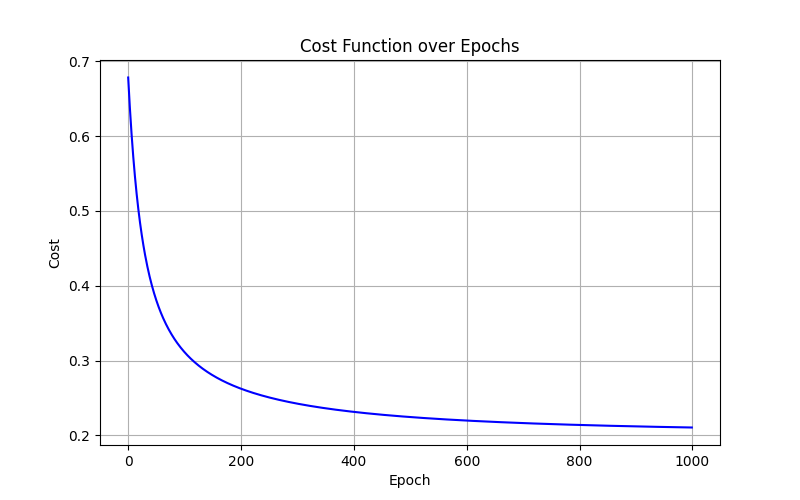
绘制决策边界:
def plot_decision_boundary_orig(data_raw, theta_final, mean, std):
plt.figure(figsize=(10, 6))
admitted = data_raw[data_raw['Admitted'] == 1]
not_admitted = data_raw[data_raw['Admitted'] == 0]
plt.scatter(admitted['Exam1'], admitted['Exam2'], c='b', marker='o', label='Admitted')
plt.scatter(not_admitted['Exam1'], not_admitted['Exam2'], c='r', marker='x', label='Not admitted')
# 原始坐标范围
x1_vals = np.linspace(data_raw['Exam1'].min(), data_raw['Exam1'].max(), 100)
# 决策边界:使用归一化过的特征 x1, x2
# 所以 x2 = (-theta0 - theta1*x1 - theta2*x2) = 0 -> 解出 x2
x1_norm = (x1_vals - mean['Exam1']) / std['Exam1']
x2_norm = (-theta_final[0, 0] - theta_final[0, 1]*x1_norm) / theta_final[0, 2]
x2_vals = x2_norm * std['Exam2'] + mean['Exam2'] # 反归一化
plt.plot(x1_vals, x2_vals, 'g-', label='Decision Boundary')
plt.xlabel('Exam 1 Score')
plt.ylabel('Exam 2 Score')
plt.title('Student Admission Prediction')
plt.legend()
plt.grid(True)
plt.show()正则化逻辑回归
数据标准化:
def normalize(self):
'''数据标准化'''
self.data[['Test1', 'Test2']] = (self.data[['Test1', 'Test2']] - self.data[['Test1', 'Test2']].mean()) / self.data[['Test1', 'Test2']].std()
passsigmoid函数:
def sigmoid(self, z):
'''sigmoid函数'''
z = np.clip(z, -500, 500) # 避免溢出
return 1 / (1 + np.exp(-z))正则化代价函数:
def cost(self, theta, X, Y):
'''代价函数'''
h = self.sigmoid(X @ theta.T) # (m, 1)
epsilon = 1e-15
h = np.clip(h, epsilon, 1 - epsilon) # 避免log(0)
return (-1 / self.m) * np.sum(Y * np.log(h) + (1 - Y) * np.log(1 - h)) # (1, 1)
def cost_regularized(self, theta, X, Y):
'''正则化代价函数'''
theta_12n = theta[:, 1:] # 第一项不需要正则化, (1, n-1)
cost = self.cost(theta, X, Y) # (1, 1)
reg = (self.lmd / (2 * self.m)) * np.sum(np.power(theta_12n, 2)) # (1, 1)
return cost + reg # (1, 1)梯度下降函数:
def gradient(self, theta, X, Y):
'''梯度中的偏导值'''
h = self.sigmoid(X @ theta.T) # (m, 1)
return (1/self.m) * X.T @ (h - Y) # (n, 1)
def gradient_regularized(self, theta, X, Y):
'''正则化梯度下降'''
gradient = self.gradient(theta, X, Y) # (n, 1)
reg = self.lmd/self.m * theta # (1, n)
reg[:, 0] = 0.0 # 第一项不需要正则化
return gradient.T + reg # (1, n)梯度计算:
def calculate(self):
'''梯度计算'''
cost = np.zeros(self.epoch)
cost_reg = np.zeros(self.epoch)
theta_final = self.theta # (1, n)
for i in range(self.epoch):
gradient = self.gradient_regularized(theta_final, self.X, self.Y) # (1, n)
theta_final = theta_final - self.rate * gradient # (1, n)
cost[i] = self.cost(theta_final, self.X, self.Y)
cost_reg[i] = self.cost_regularized(theta_final, self.X, self.Y)
return cost, cost_reg, theta_final图表/决策边界同上,这里不在赘述。
学习率α= 0.03,正则参数λ=1结果:
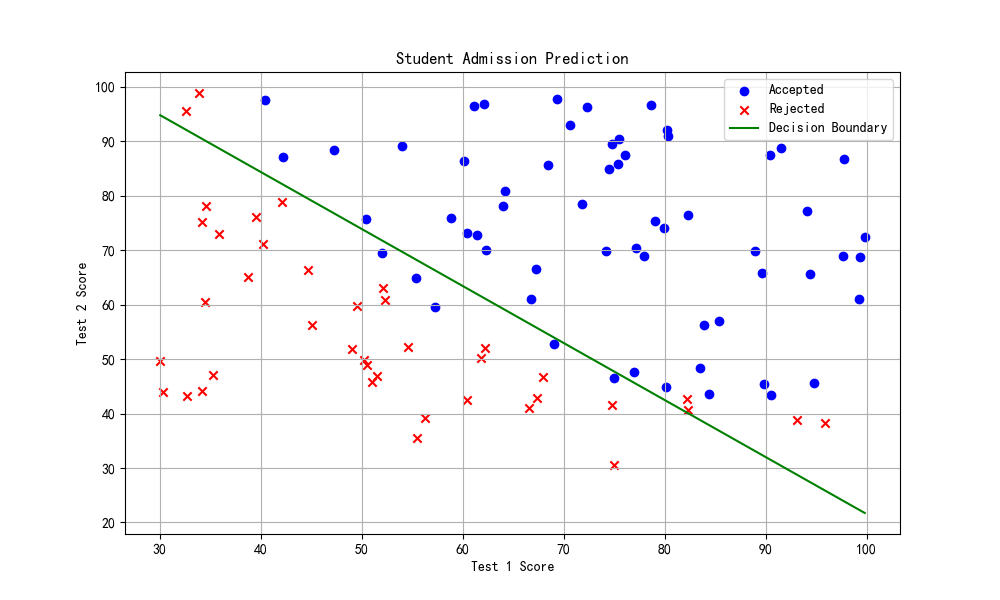
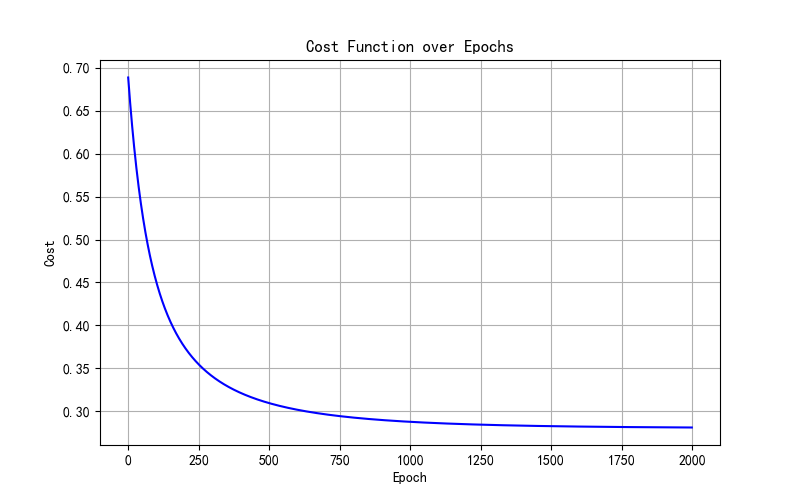
多项式逻辑回归
生成多项式特征:
from sklearn.preprocessing import PolynomialFeatures
def poly_feature(self, x1, x2, power=2):
'''
生成多项式特征
对于degree=3的情况,排序为:
- 偏置项: 1
- 1次项: x1, x2
- 2次项: x1², x1*x2, x2²
- 3次项: x1³, x1²*x2, x1*x2², x2³
即: 1, x1, x2, x1², x1*x2, x2², x1³, x1²*x2, x1*x2², x2³
'''
# 合并特征
x1_array = np.array(x1).flatten()
x2_array = np.array(x2).flatten()
X = np.column_stack([x1_array, x2_array])
# 生成多项式特征
poly = PolynomialFeatures(degree=power, include_bias=False)
X_poly = poly.fit_transform(X)
# 在每一行前插入1(偏置项)
ones = np.ones((X_poly.shape[0], 1))
X_poly_with_bias = np.column_stack([ones, X_poly])
return X_poly_with_bias # (m, 所有的特征数量)初始化:
def __init__(self,
data=[],
rate=0.001,
epoch=1000,
lmd=1,
poly_power=1,
):
'''初始化'''
self.data = data
self.data_origin = data.copy()
self.rate = rate
self.epoch = epoch
self.lmd = lmd
self.poly_power = poly_power
# 标准化
# self.normalize()
# 数据处理
self.m = self.data.shape[0]
self.n = self.data.shape[1]
self.X = self.data.iloc[:,:self.n-1] # 特征列
self.Y = self.data.iloc[:,self.n-1:] # 标签列
# 矩阵化
self.X = np.array(self.X)
self.Y = np.array(self.Y)
# 生成多项式特征(包含偏置项)
self.X = self.poly_feature(self.X[:,0], self.X[:,1], power=self.poly_power) # (m, 所有的特征数量)
# 初始化theta
self.theta = np.zeros((1, self.X.shape[1])) # (1, 所有的特征数量)
pass计算梯度函数:
def calculate(self):
'''计算梯度'''
cost_reg = np.zeros(self.epoch)
theta_final = self.theta
for i in range(self.epoch):
gradient = self.gradient_regularized(theta_final, self.X, self.Y)
theta_final = theta_final - self.rate * gradient
cost_value = self.cost_regularized(theta_final, self.X, self.Y)
cost_reg[i] = cost_value.item() if hasattr(cost_value, 'item') else cost_value
return theta_final, cost_reg绘制决策边界:
def draw_boundary(self, data_origin, theta_final):
'''绘制决策边界'''
plt.figure(figsize=(10, 6))
accepted = data_origin[data_origin['y'] == 1]
rejected = data_origin[data_origin['y'] == 0]
# 绘制数据点
plt.scatter(accepted['x1'], accepted['x2'], c='b', marker='o', label='Accepted')
plt.scatter(rejected['x1'], rejected['x2'], c='r', marker='x', label='Rejected')
# 绘制决策边界
x1 = np.linspace(data_origin['x1'].min(), data_origin['x1'].max(), 100)
x2 = np.linspace(data_origin['x2'].min(), data_origin['x2'].max(), 100)
X1, X2 = np.meshgrid(x1, x2)
Z = self.sigmoid(self.poly_feature(X1, X2, power=self.poly_power) @ theta_final.T)
Z = Z.reshape(X1.shape)
plt.contour(X1, X2, Z, levels=[0.5], colors='g')
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('工厂质量预测图')
plt.legend()
plt.show()
pass学习率α= 0.01,正则参数λ=0.8,多项式最高次数poly_power=6结果:
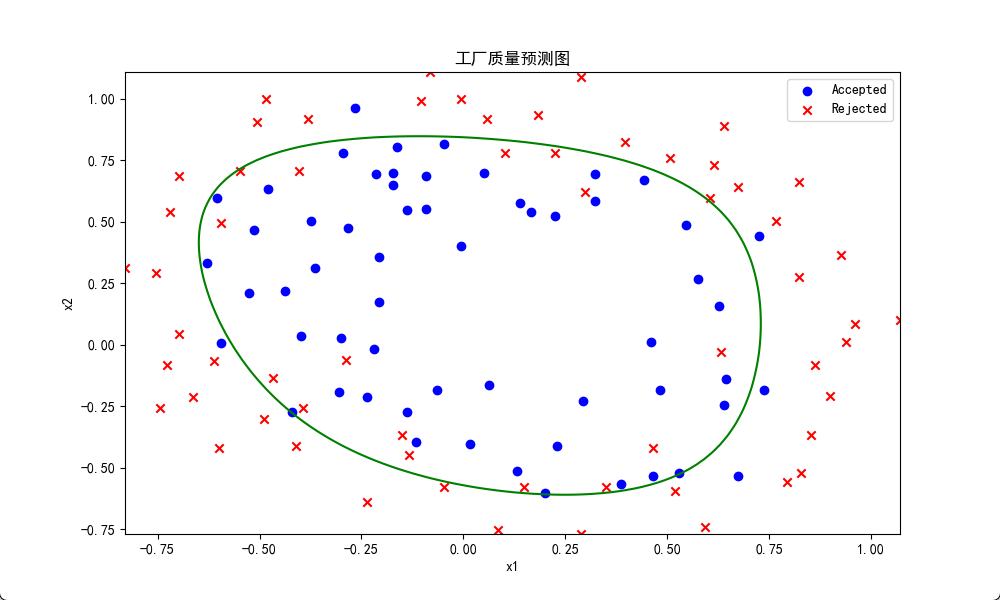
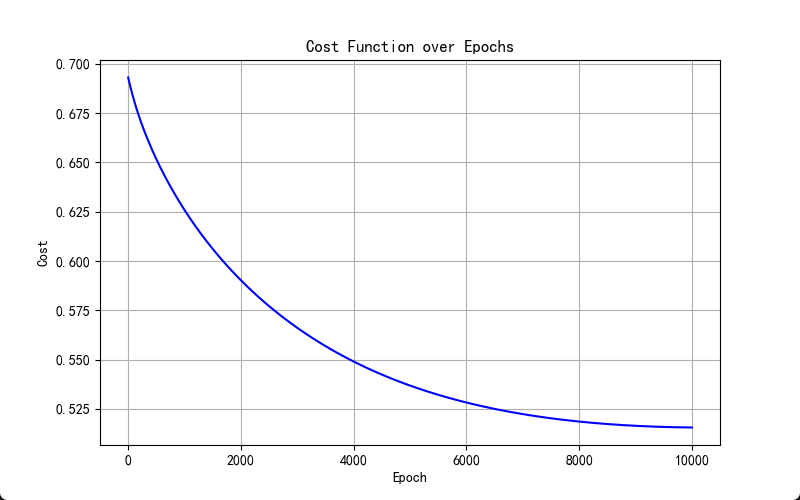
实践中的的一些错误与反思
- 数据处理代码中的
y = data.iloc[:,columns-1:columns]不能写成y = data.iloc[:,columns-1]。同样是选取最后一列,但是前者返回的是一个DataFrame(二维),np转换为矩阵为m*1;后者返回的是一个Series(一维),np转换为矩阵为1*m。
大语言学习
项目知识文档:Happy-LLM
训练集与测试集的拆分
留出法
即对数据集进行随机拆分,一部分为训练集,一部分为测试集。模型结果依赖于拆分结果,且不稳定。
k折交叉验证
即将数据集分成k份(一般为5、10),从每份中挑取一个为测试集,其余的k-1训练集,最终得到k个评价模型,对这k个模型进行平均评价,结果较为稳定。
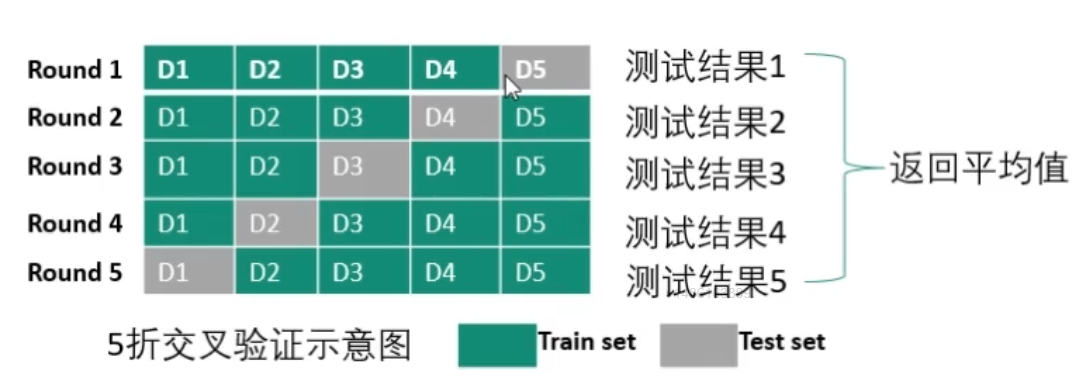
通过网格搜索调整超参数
超参数:在学习过程之前需要设置其值的一些变量,即预设值,而不是通过训练得到的参数数据。如深度学习中的学习速率等就是超参数。
网格搜索:

网格搜索结合k折交叉验证调整超参数
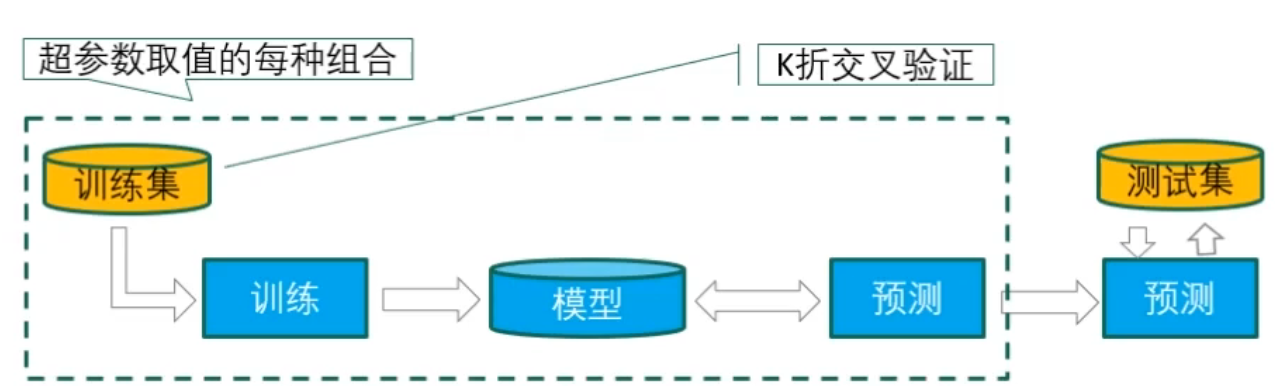
假设有A、B两个超参数值,A有3个预设值,B有5个预设值,那么总共有15个超参数对值。使用5折交叉验证拆分数据集,那么最终训练了5×15=75个模型。
神经网络
前馈神经网络(Feedforward Neural Network,FNN)
即每一层的神经元都和上下两层的每一个神经元完全连接,如图:
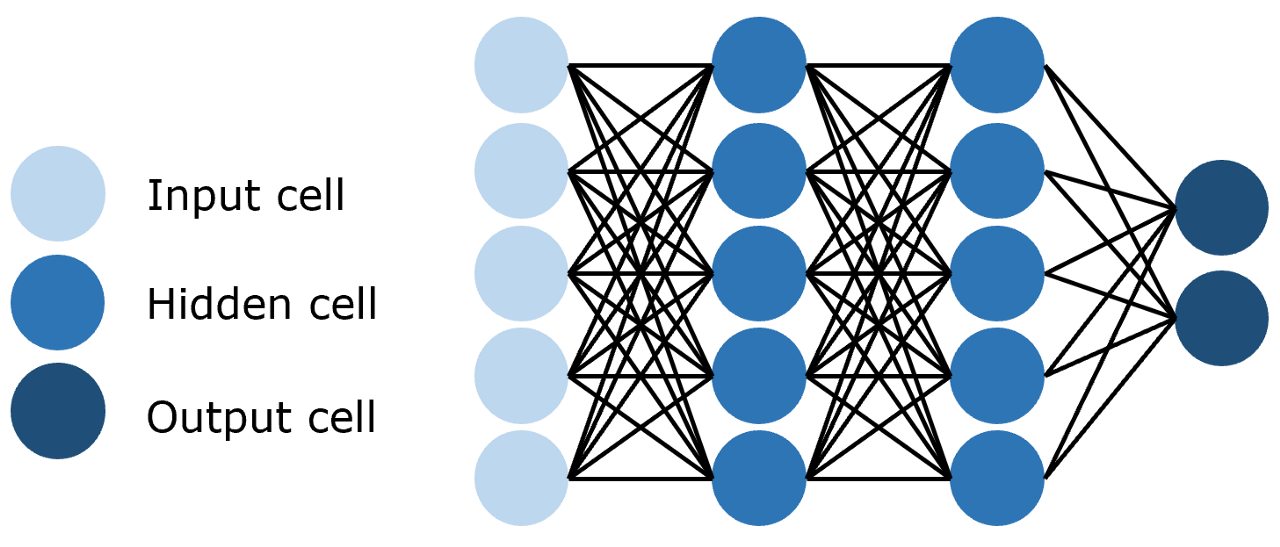
前馈神经网络的实现是较为简单的:
class MLP(nn.Module):
'''前馈神经网络'''
def __init__(self, dim: int, hidden_dim: int, dropout: float):
super().__init__()
# 定义第一层线性变换,从输入维度到隐藏维度
self.w1 = nn.Linear(dim, hidden_dim, bias=False)
# 定义第二层线性变换,从隐藏维度到输入维度
self.w2 = nn.Linear(hidden_dim, dim, bias=False)
# 定义dropout层,用于防止过拟合
self.dropout = nn.Dropout(dropout)
def forward(self, x):
# 前向传播函数
# 首先,输入x通过第一层线性变换和RELU激活函数
# 然后,结果乘以输入x通过第三层线性变换的结果
# 最后,通过第二层线性变换和dropout层
return self.dropout(self.w2(F.relu(self.w1(x))))forward函数本质就是先对输入进行一次线性变化,再非线性变化(激活函数),然后二次线性变化,最后再通过dropout层。
常见的激活函数有:
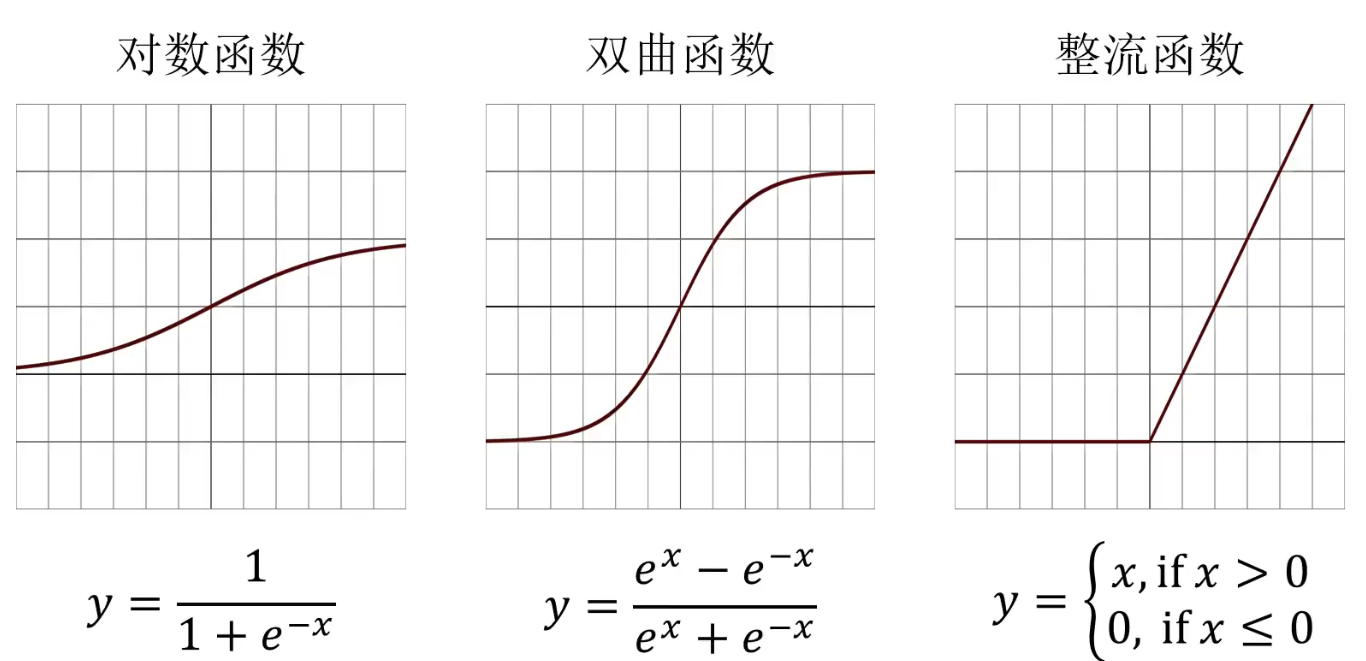
其中,整流函数也称ReLU(Rectified Linear Unit)激活函数。
卷积神经网络(Convolutional Neural Network,CNN)
即训练参数量远小于前馈神经网络的卷积层来进行特征提取和学习,如图:
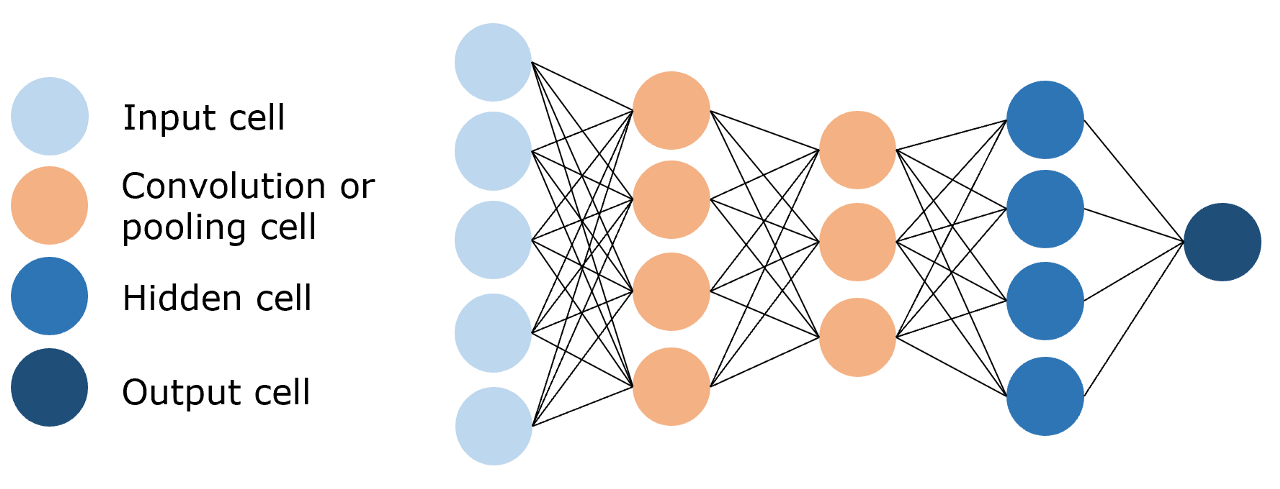
[28,28,]的图像 => conv1操作,[28,28,32],32为特征图数量 => pool1操作,[14,14,32] => conv2操作, [14,14,64] => pool2操作, [7,7,64] => fc1操作, [1,1,1024] => fc2操作,得到10个类别,即onehot编码。
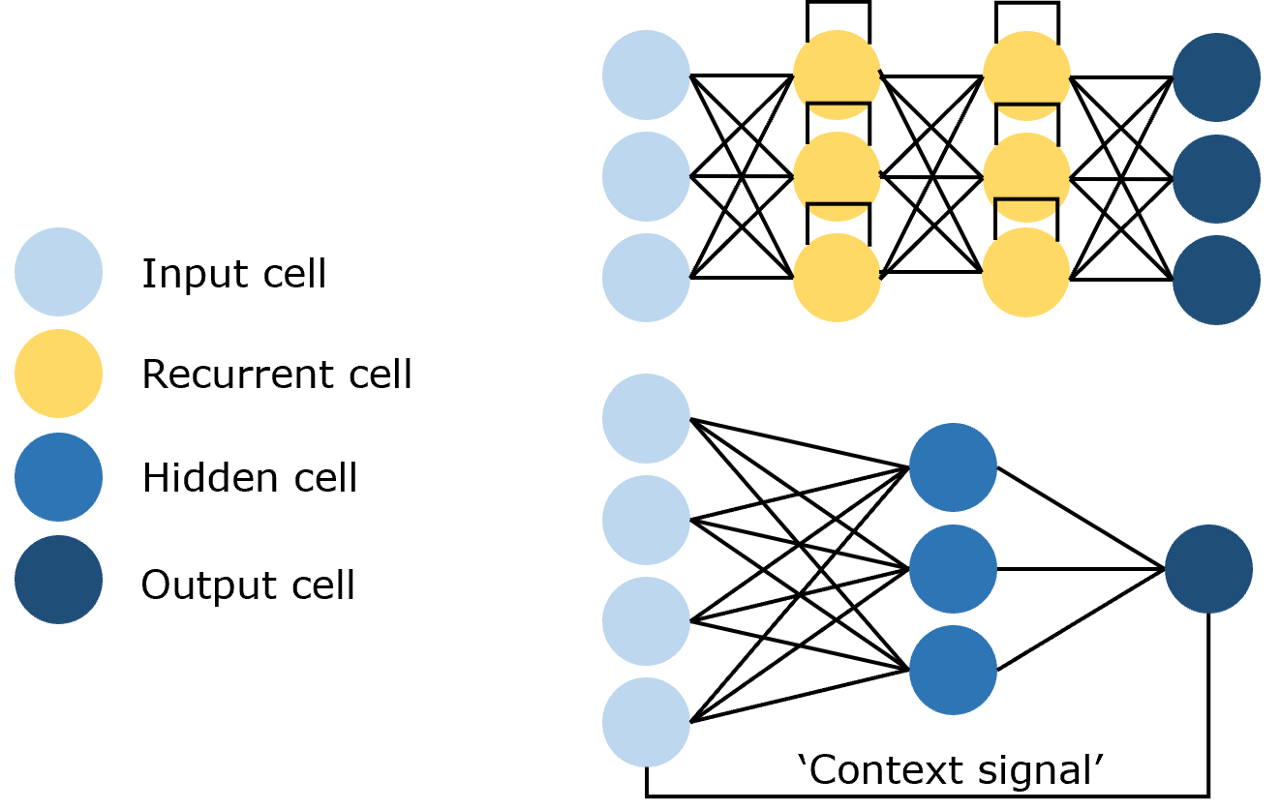
循环神经网络(Recurrent Neural Network,RNN)
能够使用历史信息作为输入、包含环和自重复的网络,如图:
NLP的任务
自然语言处理(Natural Language Processing,NLP)作为人工智能领域的一个重要分支,旨在使计算机能够理解和处理人类语言,实现人机之间的自然交流。
在NLP的广阔研究领域中,有几个核心任务构成了NLP领域的基础,它们涵盖了从文本的基本处理到复杂的语义理解和生成的各个方面。这些任务包括但不限于中文分词、子词切分、词性标注、文本分类、实体识别、关系抽取、文本摘要、机器翻译以及自动问答系统的开发。每一项任务都有其特定的挑战和应用场景,它们共同推动了语言技术的发展,为处理和分析日益增长的文本数据提供了强大的工具。
详见NLP任务。
Encoder – Decoder
Encoder 和 Decoder 内部传统神经网络的经典结构——前馈神经网络(FNN)、层归一化(Layer Norm)和残差连接(Residual Connection)
前馈神经网络(FNN)
每一个 Encoder Layer 都包含一个上文讲的注意力机制和一个前馈神经网络。
层归一化(Layer Norm)
是深度学习中经典的归一化操作。神经网络主流的归一化一般有两种,批归一化(Batch Norm)和层归一化(Layer Norm)。
归一化核心是为了让不同层输入的取值范围或者分布能够比较一致。

相较于 Batch Norm 在每一层统计所有样本的均值和方差,Layer Norm 在每个样本上计算其所有层的均值和方差,从而使每个样本的分布达到稳定。Layer Norm 的归一化方式其实和 Batch Norm 是完全一样的,只是统计统计量的维度不同。
简单地实现一个 Layer Norm 层:
class LayerNorm(nn.Module):
''' Layer Norm 层'''
def __init__(self, features, eps=1e-6):
super(LayerNorm, self).__init__()
# 线性矩阵做映射
self.a_2 = nn.Parameter(torch.ones(features))
self.b_2 = nn.Parameter(torch.zeros(features))
self.eps = eps
def forward(self, x):
# 在统计每个样本所有维度的值,求均值和方差
mean = x.mean(-1, keepdim=True) # mean: [bsz, max_len, 1]
std = x.std(-1, keepdim=True) # std: [bsz, max_len, 1]
# 注意这里也在最后一个维度发生了广播
return self.a_2 * (x - mean) / (std + self.eps) + self.b_2残差连接(Residual Connection)
为了避免模型退化,Transformer 采用了残差连接的思想来连接每一个子层。
残差连接,即下一层的输入不仅是上一层的输出,还包括上一层的输入。残差连接允许最底层信息直接传到最高层,让高层专注于残差的学习。
例如,在 Encoder 中,在第一个子层,输入进入多头自注意力层的同时会直接传递到该层的输出,然后该层的输出会与原输入相加,再进行标准化。在第二个子层也是一样。即:
x=x+MultiHeadSelfAttention(LayerNorm(x))
output=x+FNN(LayerNorm(x))output=x+FNN(LayerNorm(x))
在代码实现中,通过在层的 forward 计算中加上原值来实现残差连接:
# 注意力计算
h = x + self.attention.forward(self.attention_norm(x))
# 经过前馈神经网络
out = h + self.feed_forward.forward(self.fnn_norm(h))Encoder
在实现上述组件之后,我们可以搭建起 Transformer 的 Encoder。Encoder 由 N 个 Encoder Layer 组成,每一个 Encoder Layer 包括一个注意力层和一个前馈神经网络。因此,我们可以首先实现一个 Encoder Layer:
class EncoderLayer(nn.Module):
'''Encoder层'''
def __init__(self, args):
super().__init__()
# 一个 Layer 中有两个 LayerNorm,分别在 Attention 之前和 MLP 之前
self.attention_norm = LayerNorm(args.n_embd)
# Encoder 不需要掩码,传入 is_causal=False
self.attention = MultiHeadAttention(args, is_causal=False)
self.fnn_norm = LayerNorm(args.n_embd)
self.feed_forward = MLP(args)
def forward(self, x):
# Layer Norm
norm_x = self.attention_norm(x)
# 自注意力
h = x + self.attention.forward(norm_x, norm_x, norm_x)
# 经过前馈神经网络
out = h + self.feed_forward.forward(self.fnn_norm(h))
return out然后我们搭建一个 Encoder,由 N 个 Encoder Layer 组成,在最后会加入一个 Layer Norm 实现规范化:
class Encoder(nn.Module):
'''Encoder 块'''
def __init__(self, args):
super(Encoder, self).__init__()
# 一个 Encoder 由 N 个 Encoder Layer 组成
self.layers = nn.ModuleList([EncoderLayer(args) for _ in range(args.n_layer)])
self.norm = LayerNorm(args.n_embd)
def forward(self, x):
"分别通过 N 层 Encoder Layer"
for layer in self.layers:
x = layer(x)
return self.norm(x)通过 Encoder 的输出,就是输入编码之后的结果。
Decoder
类似的,我们也可以先搭建 Decoder Layer,再将 N 个 Decoder Layer 组装为 Decoder。
但是和 Encoder 不同的是,Decoder 由两个注意力层和一个前馈神经网络组成。第一个注意力层是一个掩码自注意力层,即使用 Mask 的注意力计算,保证每一个 token 只能使用该 token 之前的注意力分数;第二个注意力层是一个多头注意力层,该层将使用第一个注意力层的输出作为 query,使用 Encoder 的输出作为 key 和 value,来计算注意力分数。
最后,再经过前馈神经网络:
class DecoderLayer(nn.Module):
'''解码层'''
def __init__(self, args):
super().__init__()
# 一个 Layer 中有三个 LayerNorm,分别在 Mask Attention 之前、Self Attention 之前和 MLP 之前
self.attention_norm_1 = LayerNorm(args.n_embd)
# Decoder 的第一个部分是 Mask Attention,传入 is_causal=True
self.mask_attention = MultiHeadAttention(args, is_causal=True)
self.attention_norm_2 = LayerNorm(args.n_embd)
# Decoder 的第二个部分是 类似于 Encoder 的 Attention,传入 is_causal=False
self.attention = MultiHeadAttention(args, is_causal=False)
self.ffn_norm = LayerNorm(args.n_embd)
# 第三个部分是 MLP
self.feed_forward = MLP(args)
def forward(self, x, enc_out):
# Layer Norm
norm_x = self.attention_norm_1(x)
# 掩码自注意力
x = x + self.mask_attention.forward(norm_x, norm_x, norm_x)
# 多头注意力
norm_x = self.attention_norm_2(x)
h = x + self.attention.forward(norm_x, enc_out, enc_out)
# 经过前馈神经网络
out = h + self.feed_forward.forward(self.ffn_norm(h))
return out然后同样的,我们搭建一个 Decoder 块:
class Decoder(nn.Module):
'''解码器'''
def __init__(self, args):
super(Decoder, self).__init__()
# 一个 Decoder 由 N 个 Decoder Layer 组成
self.layers = nn.ModuleList([DecoderLayer(args) for _ in range(args.n_layer)])
self.norm = LayerNorm(args.n_embd)
def forward(self, x, enc_out):
"Pass the input (and mask) through each layer in turn."
for layer in self.layers:
x = layer(x, enc_out)
return self.norm(x)完成上述 Encoder、Decoder 的搭建,就完成了 Transformer 的核心部分,接下来将 Encoder、Decoder 拼接起来再加入 Embedding 层就可以搭建出完整的 Transformer 模型啦。